Jump to: Discrete energy and radioactivity 7.1 Nuclear reactions 7.2 The structure of matter 7.3 Topic 7 Problems

7.1 Discrete energy and radioactivity

Energy levels

Electrons can only occupy specific energy levels. The energy levels are said to be quantized.

Hydrogen energy levels:

Energy level (n) Energy/eV
1 -13.58
2 -3.39
3 -1.51
4 -0.85
5 -0.54

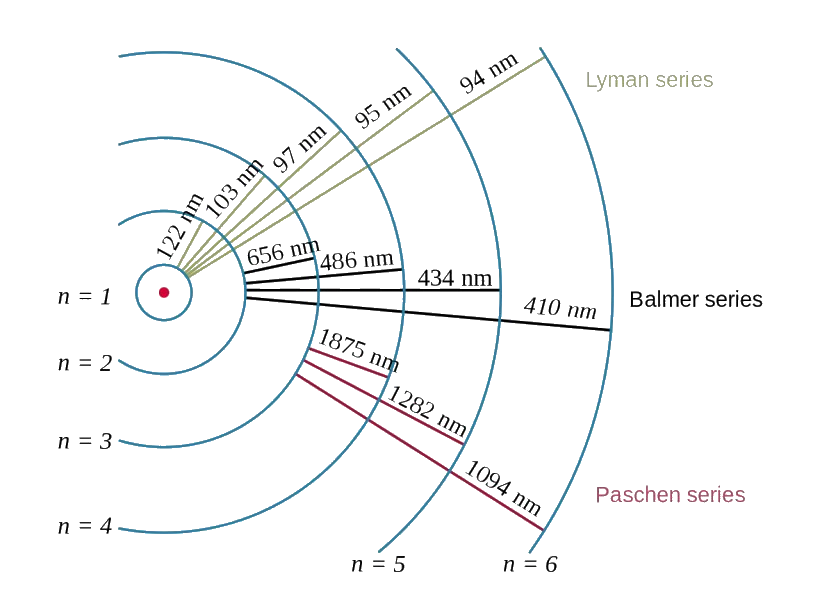
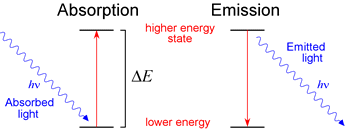
For an electron to jump energy levels it needs some energy. It must be exactly the right amount of energy. An excited electron absorbs a photon. When the electron jumps to the lower energy level, it emits a photon of a specific frequency.

\begin{gather} E=hf\\ E=energy\ carried\ by\ a\ photon,\ h=Planck\ constant\ \left( 6.63x10^{-34} \ Js\right) \notag\\ f=frequency \notag \end{gather}

Emission spectra

The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to an atom or molecule making a transition from a high energy state to a lower energy state.

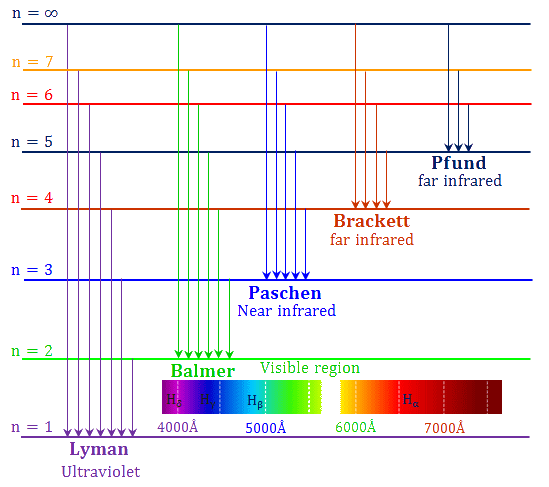
Absorption spectra

The electrons in atoms can also get excited by absorbing photons. This creates a continuous spectrum streaked with a couple dark lines that correspond to the frequency of the emission photons.

Video explanation

Radioactive decay

Radioactive decay is a naturally occurring process in which the nucleus of an unstable atom will spontaneously change into a different nuclear configuration by the emission of combinations of alpha, beta and gamma radiation.

The nuclide decaying is called the parent and the nuclide(s) formed are called daugher(s).

*Isotopes are variants of a particular chemical element which differ in neutron number, and consequently in nucleon number. All isotopes of a given element have the same number of protons but different numbers of neutrons in each atom.

\begin{gather} ^{A}_{Z} X\\ A=mass\ number,\ Z=atomic\ number \notag \end{gather}

Due to conservation of mass, energy and charge, the equation must balance so that there is an equal number of nucleons on each side.

Alpha (α) decay

In alpha decay, a nuclide emits a particle of the same configuration as a helium nucleus.

Examples:

\begin{gather} ^{238}_{\ \ 92} U\rightarrow ^{4}_{2} He+^{234}_{\ \ 90} Th\\ ^{234}_{\ \ 90} Th\rightarrow ^{4}_{2} He+^{230}_{\ \ 88} Ra \notag\\ \notag \end{gather}
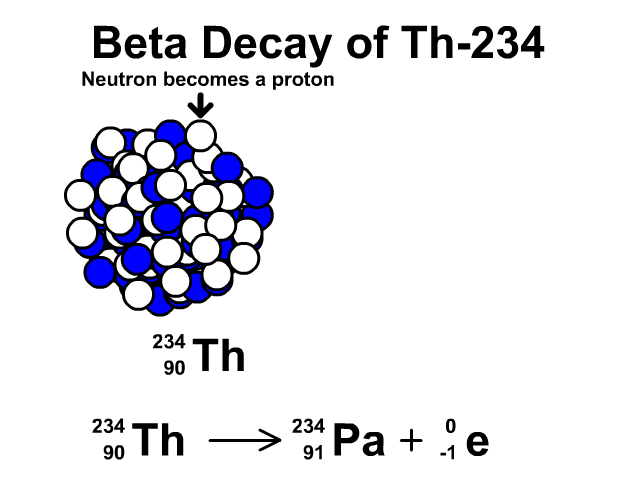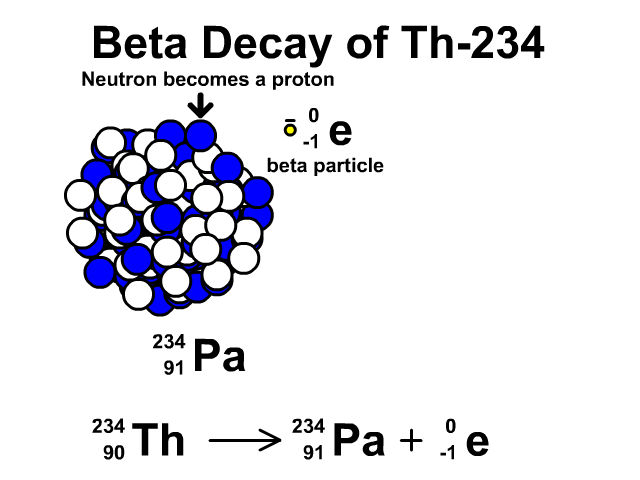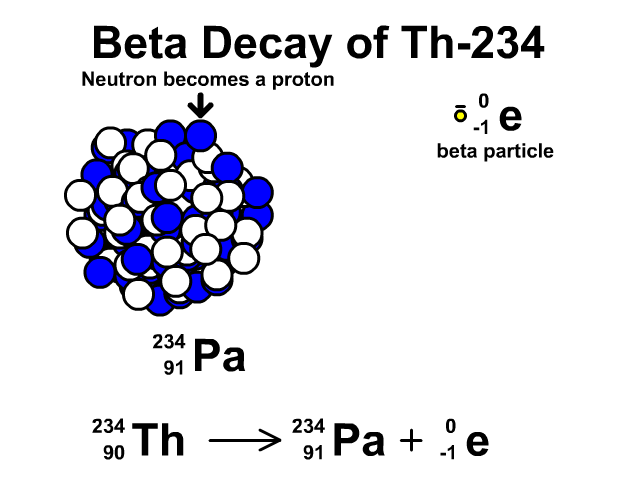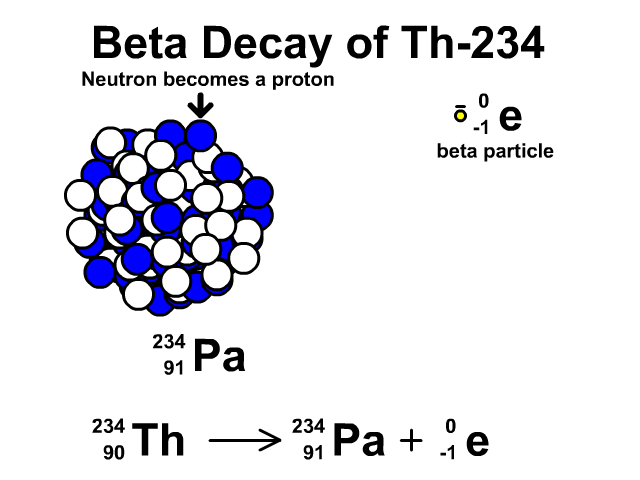
Negative beta (β-) decay

In negative beta decay, an unstable nuclide emits an electron. A neutron is converted into a proton. Furthermore, this is accompanied by an electron antineutrino.

Examples:

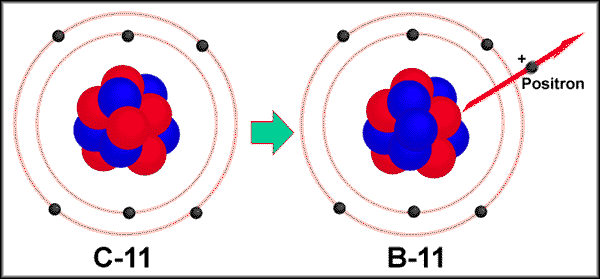
\begin{gather} ^{131}_{\ \ 53} I\rightarrow ^{\ \ 0}_{-1} e+^{131}_{\ \ 54} Xe+^{\ \ 0}_{\ \ 0}\overline{v}\\ ^{234}_{\ \ 90} Th\rightarrow ^{\ \ 0}_{-1} e+^{234}_{\ \ 91} Pa+^{\ \ \ \ 0}_{\ \ \ \ 0}\overline{v} \notag\\ \notag \end{gather}
Positron beta (β+) decay

In positive beta decay, an unstable nuclide emits a positron (antiparticle of electron). A proton is converted into a neutron. Furthermore, this decay is accompanied by an electron neutrino.

Examples:

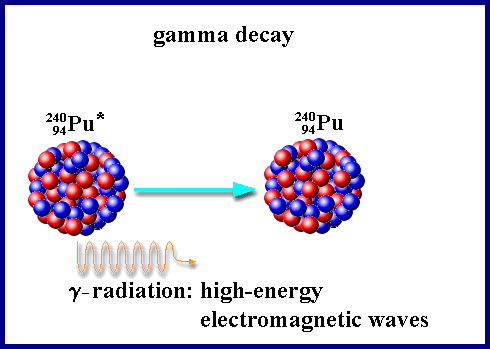
\begin{gather} \ ^{11}_{\ \ 6} C\rightarrow ^{\ \ 0}_{+1} e+^{\ 11}_{\ \ \ 5} B+^{\ \ 0}_{\ \ 0} v\\ ^{\ \ 21}_{\ \ 11} Na\rightarrow ^{\ \ 0}_{+1} e+^{\ \ 21}_{\ \ 10} Ne+^{\ \ \ \ 0}_{\ \ \ \ 0} v \notag\\ \notag \end{gather}
Gamma ray (γ) emission

Gamma rays are high-energy photons often accompanying other decay mechanisms. After emitting a beta or alpha particle, the nucleus is left in an excited state. It stabilises by emitting gamma photons, thus losing excess energy.

Examples:

\begin{gather} \ ^{60}_{\ \ 27} Co\rightarrow ^{\ \ 0}_{-1} e+^{\ \ \ 60}_{\ \ \ 28} Ni^{*} +^{\ \ 0}_{\ \ 0}\overline{v} +^{\ \ 0}_{\ \ 0} \gamma \\ ^{\ \ \ 60}_{\ \ \ 28} Ni^{*}\rightarrow ^{\ \ \ 60}_{\ \ \ 28} Ni+^{\ \ 0}_{\ \ 0} \gamma \notag\\ Thus\ the\ full\ decay\ of\ cobalt-60\ is: \notag\\ \ ^{60}_{\ \ 27} Co\rightarrow ^{\ \ 0}_{-1} e+^{\ \ \ 60}_{\ \ \ 28} Ni+^{\ \ 0}_{\ \ 0}\overline{v} +2\gamma \notag \end{gather}
Stable and Unstable Nuclei
Radiation vs Radioactive Atoms

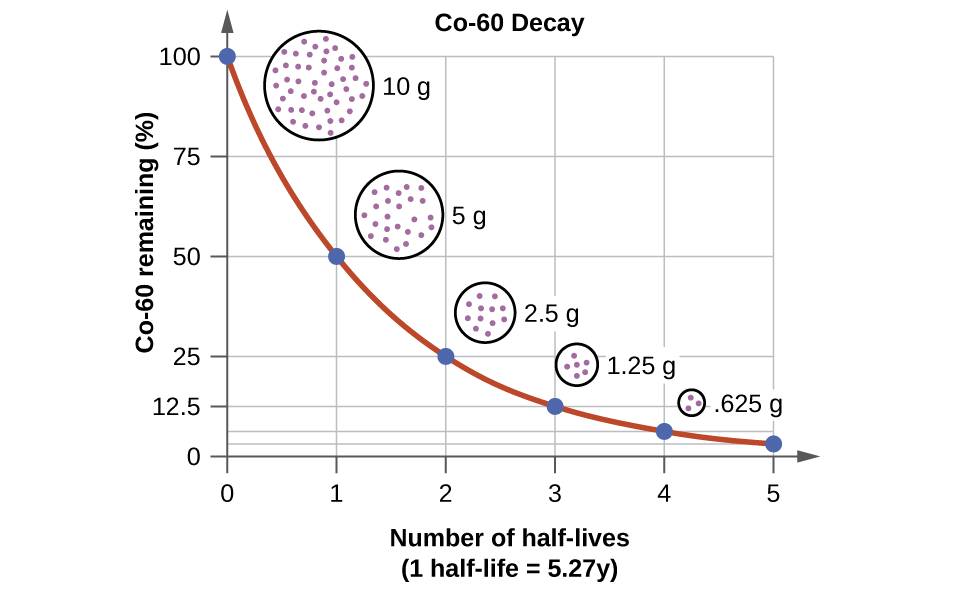
Half-life

Radioactive decay is a continous but random process. A nuclide has a constant probability of decay, which does not depend on the size of the sample. Another way to look at this is half-life.

The radioactive half-life of a substance is the time it takes for half of its radioactive nuclei to decay or for the initial activity of a sample to fall by half.

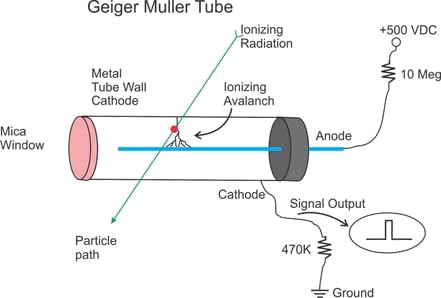
\begin{gather} N( t) =N_{0}\left(\frac{1}{2}\right)^{\frac{t}{t_{1/2}}}\\ N( t) =quantity\ of\ substance\ remaining,\ N_{0} =initial\ quantity\ of\ the\ substance \notag\\ t=time\ elapsed,\ t_{1/2} =halflife\ of\ the\ substance \notag\\ \notag\\ \notag \end{gather}
Video explanation
Measuring radioactive decay

For beta and gamma radiation, the count rate near to a source is measured using a Geiger counter (G-M tube). Alpha particles can be detected using a spark counter.

Green Uranium Glass an other things measured with Geiger counter

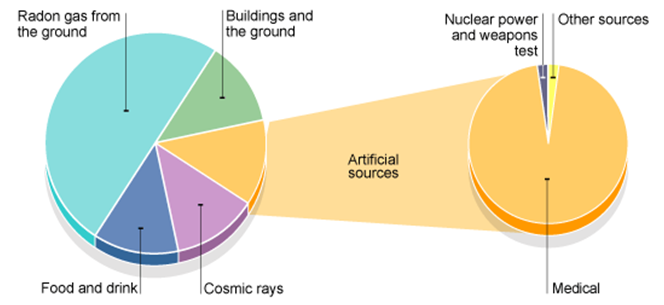
Background count

The G-M tube will give a reading even when a source of radioactivity is not present. It will be measuring the background count.

Natural sources: cosmic rays from space, radioactive rocks and soil, living organisms that have consumed radioactive substances in the food chain.

Artificial sources: radioactive waste from nuclear power plants, radioactive fallout from nuclear weapons, medical x-rays.

The Most Radioactive Places on Earth

Absorption of radiation

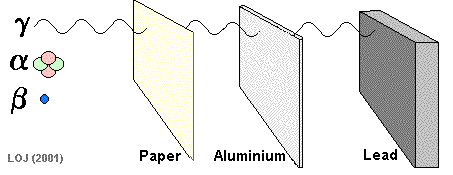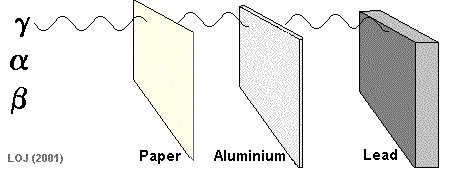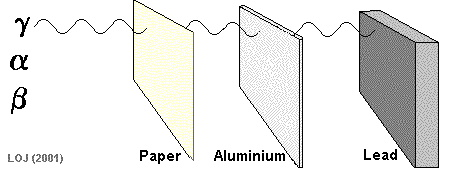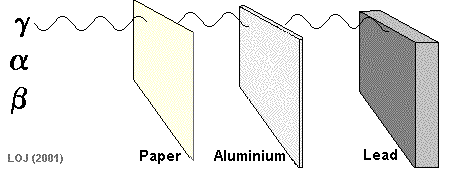
Emission Composition Range Ionizing ability
α a helium nucleus (2 protons & 2 neutrons) low penetration, biggest mass and charge, aborbed by a few centimetres of air, skin or thin sheet of paper very highly ionizing
β high energy electrons & positrons moderate penetration, most are absorbed by 25cm of air, a few centimetres of body tissue or a few milimetres of metals, such as aluminium. moderately highly ionizing
γ very high frequency EM radiation highly penetrating, most photons are absorbed by a few cm of lead or several meters of concrete poorly ionizing, usually secondary ionization by electrons that the photons can eject from metals

7.2 Nuclear reaction

The unified atomic mass unit

The unified atomic mass unit (u) is defined as 1/12 of the rest mass of an unbound atom of carbon-12 in its nuclear and electronic ground state.

It has a value of 1.661 x10-27 kg.

Mass defect and nuclear binding energy

The nuclear binding energy of a nucleus is the amount of work required to separate the nucleons inside the nucleus.

\begin{gather} Binding\ energy\ per\ nucleon=\frac{\ binding\ energy\ of\ nucleus}{number\ of\ nucleons\ in\ nucleus}\\ \notag \end{gather}

Mass and energy are different aspects of the same quantity:

\begin{gather} E=mc^{2}\\ E=energy,\ m=mass,\ c=speed\ of\ light\ in\ vacuum \notag\\ \notag \end{gather}

The total mass of the individual nucleons making up a nucleus must be greater than the mass of that nucleus, since work needs to be done in order to break the nucleus into its component parts.

This difference is the mass defect.

Einstein's Proof of E=mc²
Mass and energy units for nuclear changes

The nuclear energy is often measured in MeV (eV x 106).

The unified atomic mass unit can also be written as 931.5 MeV c-2. To find the equivalent energy in MeV, multiply by c2.

Variation of nuclear binding energy per nucleon

The nuclear binding energy tends to be larger for larger nuclei, and smaller for smaller nuclei. This is because, with a greater number of nucleons, there are more opportunities for the strong force to act between nucleons.

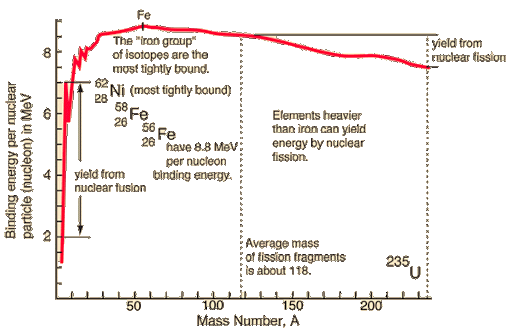Binding energy

Nuclear fusion

Nuclear fusion is a reaction in which two or more atomic nuclei are combined to form one or more different atomic nuclei and subatomic particles (neutrons or protons). The total nuclear binding energy of the fused nuclei is greater than the sum of total nuclear binding energies of component nuclei, releases energy.

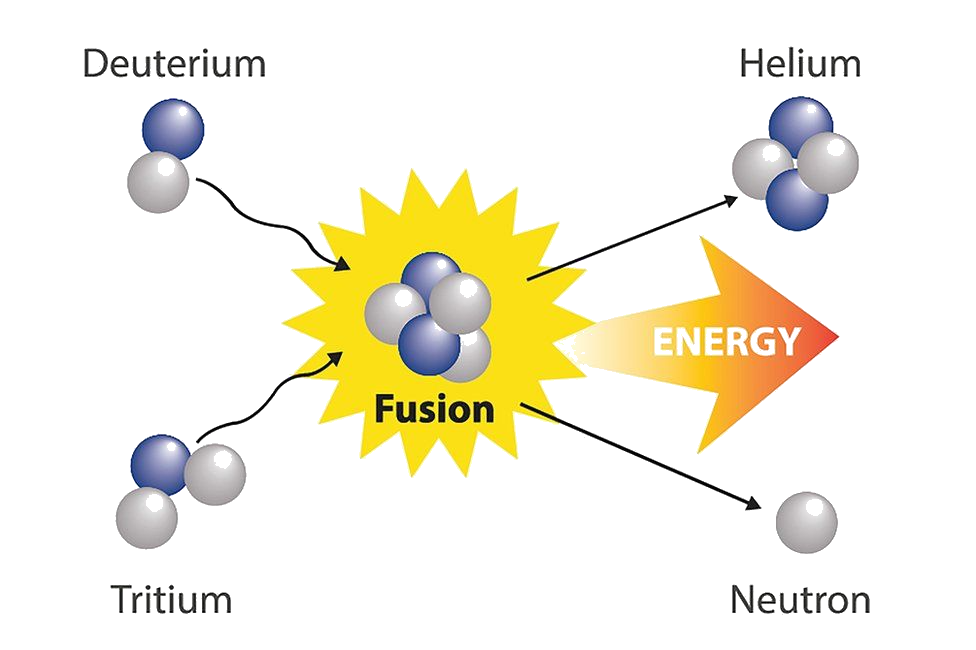
Since the total number of nucleons in conserved, m3 has a smaller mass than the total for m1 + m2.

\begin{gather} \Delta E=(( m_{1} +m_{2}) -m_{3}) c^{2}\\ \notag\\ \Delta E=kinetic\ energy\ emitted,\ c=speed\ of\ light\ in\ vacuum \notag\\ m=mass \notag \end{gather}

Nuclear fission

Nuclear fission is a nuclear reaction or a radioactive decay process in which the nucleus of an atom splits into two or more smaller, lighter nuclei. The fission process often produces gamma photons, and releases a very large amount of energy.

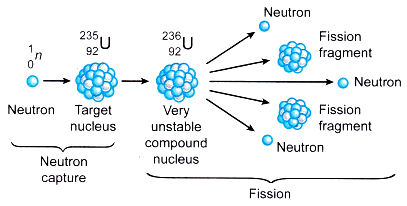\begin{gather} \Delta E=( m_{3} -( m_{1} +m_{2})) c^{2}\\ \notag\\ \Delta E=kinetic\ energy\ emitted,\ c=speed\ of\ light\ in\ vacuum \notag\\ m=mass \notag \end{gather}
Fission and fusion

7.3 The structure of matter

Classification of particles - the standard model

Each particle also has an antimatter counterpart. When matter collides with its corresponding antimatter, the particles annihilate and release energy by mass-energy equivalence.

Leptons

A lepton is an elementary particle of half-integer spin (spin ​1/2) that does not undergo strong interactions. They are members of the electron family.

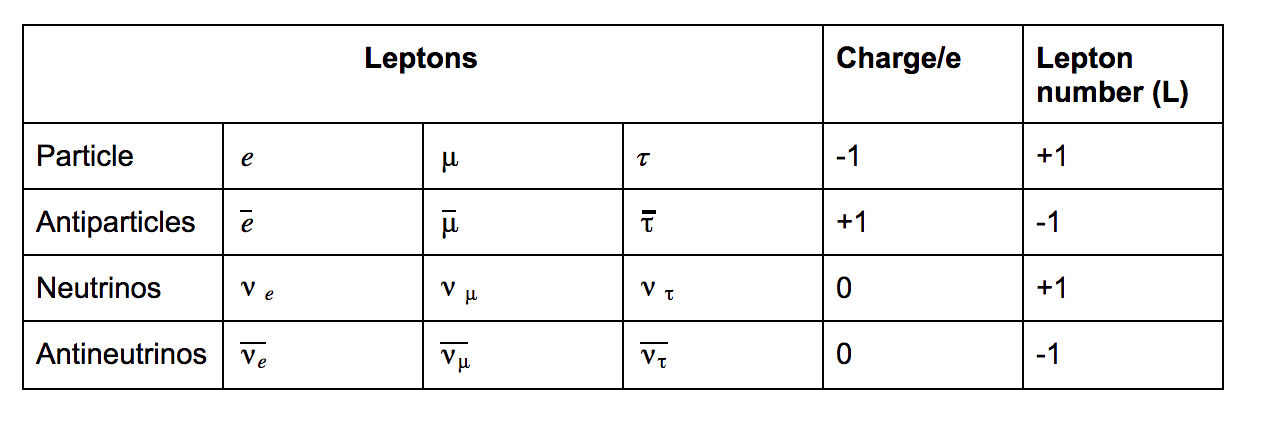
Quarks

A quark is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. There are six types, known as flavors, of quarks: up, down, strange, charm, bottom, and top.

Quark confinement

Hadrons are formed from a combination of 2 or 3 quarks (mesons and baryons), which is known as quark confinement. The quarks are held in place with gluons.

Explanation of quark confinement in detail
Hadrons

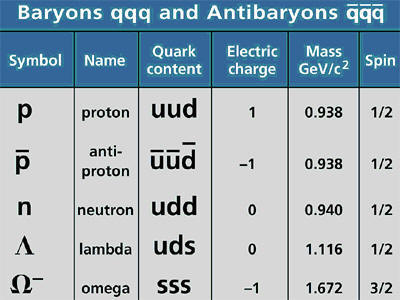
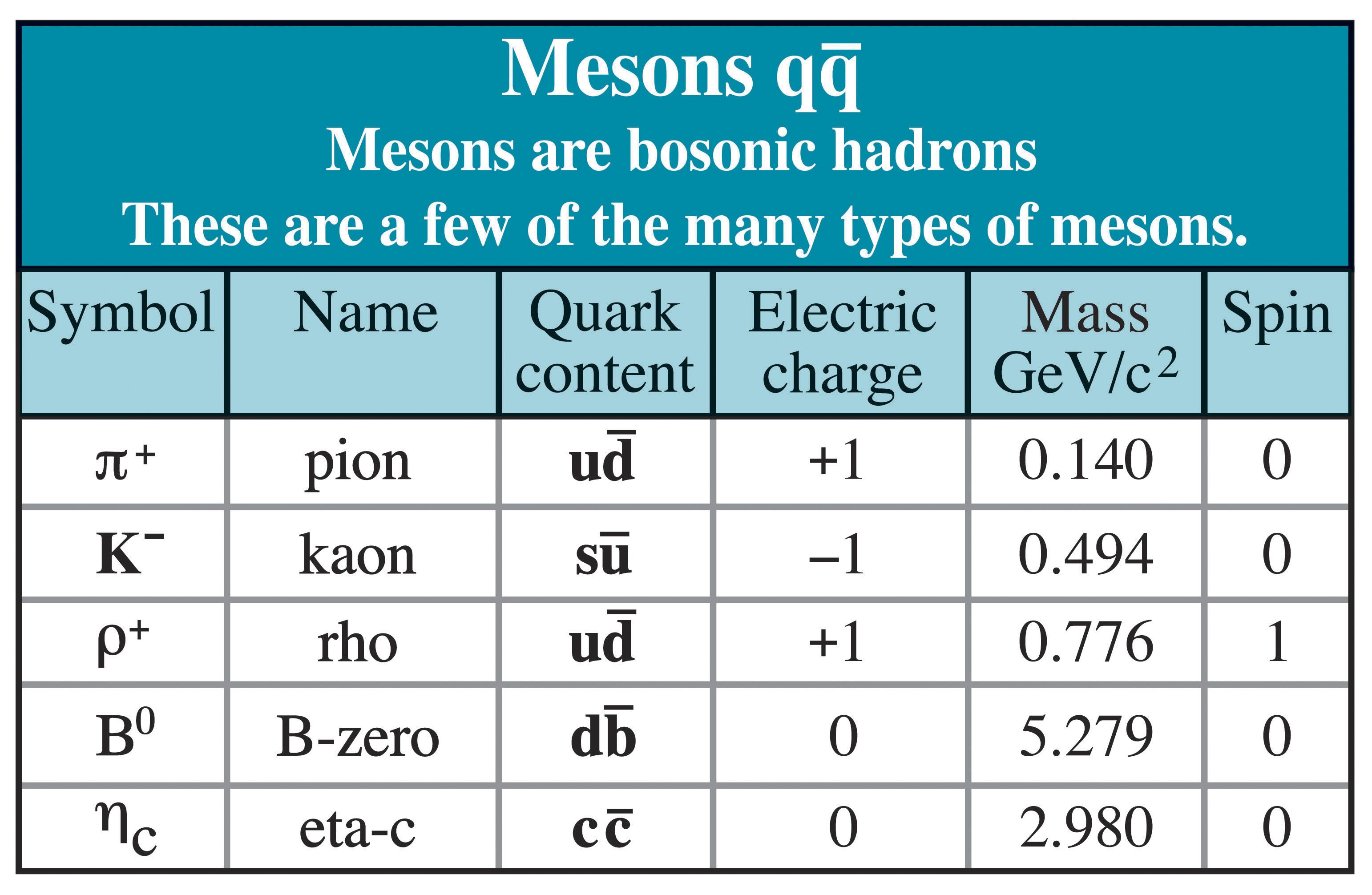
Hadrons are sub-divided into baryons and mesons.

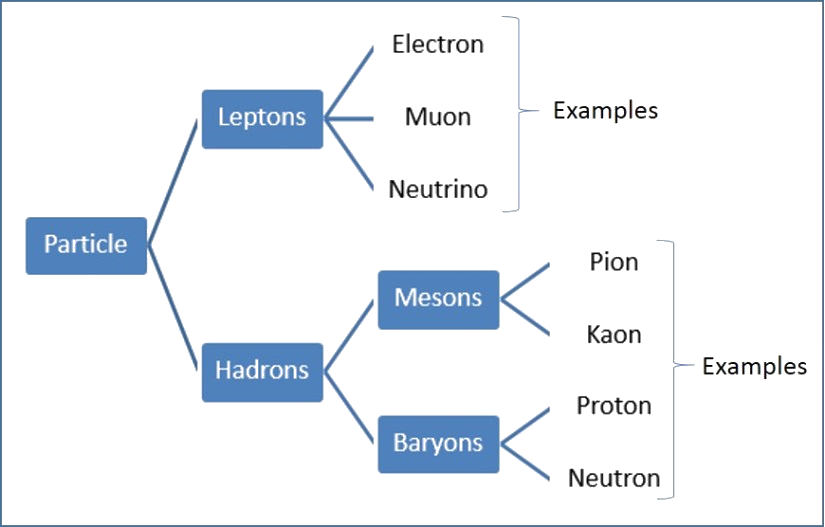
Baryons
Mesons
Conservation rules

The baryon number (B) and lepton number (L) must be conserved. All leptons have a lepton number of +1 and all antileptons have a lepton number of -1.

An interaction or decay is feasible based on the conservation rules (common IB question).

Example 1:

\begin{gather} p+\pi ^{-}\rightarrow n+\pi ^{0}\\ Q:\ +1-1\rightarrow 0+0\ \ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ B:+1+0\rightarrow +1+0\ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ L:\ 0+0\rightarrow 0+0\ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ This\ interaction\ is\ possible. \notag \end{gather}

Example 2:

\begin{gather} p+p\rightarrow p+p+n\\ Q:\ +1+1\rightarrow +1+1+0\ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ B:+1+1\rightarrow +1+1+1\ \ \textcolor[rgb]{0.82,0.01,0.11}{\ incorrect} \notag\\ L:\ 0+0\rightarrow 0+0+0\ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ This\ interaction\ fails\ because\ of\ the\ baryon\ number. \notag \end{gather}
The standard model- video explanation

Fundamental forces

Fundamental interactions, also known as fundamental forces, are the interactions that do not appear to be reducible to more basic interactions.

Force Range Relative strenght Roles played by the forces in the universe
Gravitational ∞ 1 binding planets, solar system, sun, stars, galaxies
Weak nuclear 10-18 m 1024 (W+, W-) transmutation of elements (W0), supernovae
Electromagnetic ∞ 1035 binding atoms, magnetic fields
Strong nuclear 10-15 m 1037 binding atomic nuclei, fusion processes in stars
Video explanation

Exchange particles

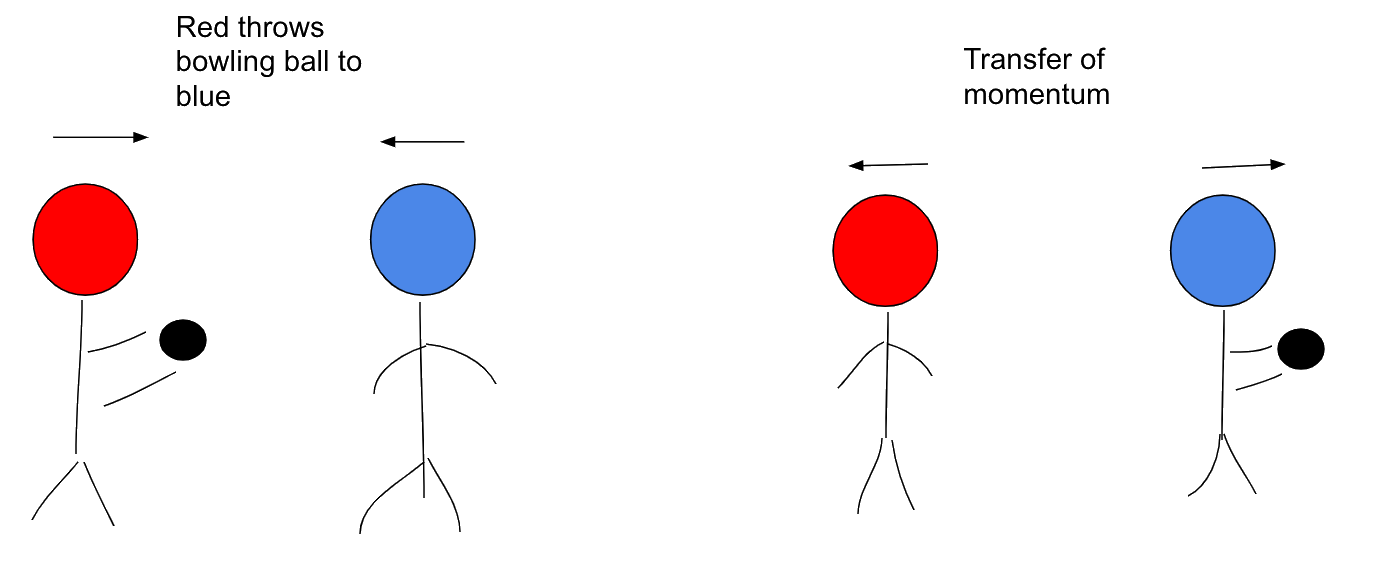
In 1935, Hideki Yukawa proposed that force between a pair of particles is transmitted by gauge bosons.

The exchange particles are "virtual", as they cannot be detected during the exchange, since detection would imply that it no longer acts as a mediator of the force between two particles.

The larger the rest mass of the exchange particle, the lower the time it can transmit the force without being detected, therefore the lower the range of the force.

The virtual particle exchanges momentum between two particles in a classical mechanics way. It works similar to throwing a bowling ball to a friend when ice skating.

Force Exchange particle Acts on
Gravitatonal gravitons (theoretical) all particles
Weak nuclear W+, W- and Z0 bosons quarks and leptons
Electromagnetic photons charged particles
Strong nuclear gluons (and mesons) quarks, gluons and hadrons
IB Physics: Exchange Particles

Feynman diagrams

Feynman diagrams are graphical visualisations of interactions betweeen particles.

Straight lines represent particles. Upwards arrows represent a particle moving forwards in time, downward arrows represent an antiparticle moving fowards in time. Wavy lines represent exchange particles.

The x-axis represents position, and the y-axis represents time, but these two are interchangeable.

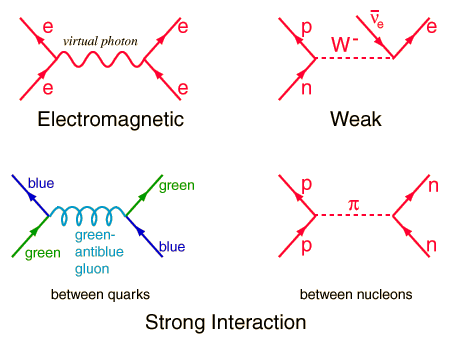Video explanation of Feynman diagrams Surely You're Joking, Mr. Feynman! - great book. (OPTIONAL)

Conservation of strangeness

Strangeness is not conserved when strange particles decay through the weak interaction.

Strangeness is conserved in strong interactions and electromagnetic interactions.

Examples:

\begin{gather} {p+\pi ^{-}}\rightarrow K^{0} +\Lambda ^{0}\\ Q:\ \left( +\frac{2}{3} +\frac{2}{3} -\frac{1}{3}\right) +\left( -\frac{2}{3} -\frac{1}{3}\right) =\left( -\frac{1}{3} -\frac{1}{3}\right) +\left( +\frac{2}{3} -\frac{1}{3} -\frac{1}{3}\right) \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ L:0=0\ ( none\ of\ the\ particles\ are\ leptons) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ B:\left( +\frac{1}{3} +\frac{1}{3} +\frac{1}{3}\right) +\left( +\frac{1}{3} +\frac{1}{3}\right) =\left( +\frac{1}{3} +\frac{1}{3}\right) +\left( +\frac{1}{3} +\frac{1}{3} +\frac{1}{3}\right)\textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ S:\ 0=-1+1\ \textcolor[rgb]{0.49,0.83,0.13}{correct} \notag\\ The\ interaction\ is\ viable \notag \end{gather}

The Higgs boson

The Higgs boson is an elementary particle in the Standard Model of particle physics, produced by the quantum excitation of the Higgs field,[8][9] one of the fields in particle physics theory.[9] It is named after physicist Peter Higgs, who in 1964, along with five other scientists, proposed the Higgs mechanism to explain why particles have mass.

Discovered in 2012 at CERN.

Basics of the Higgs boson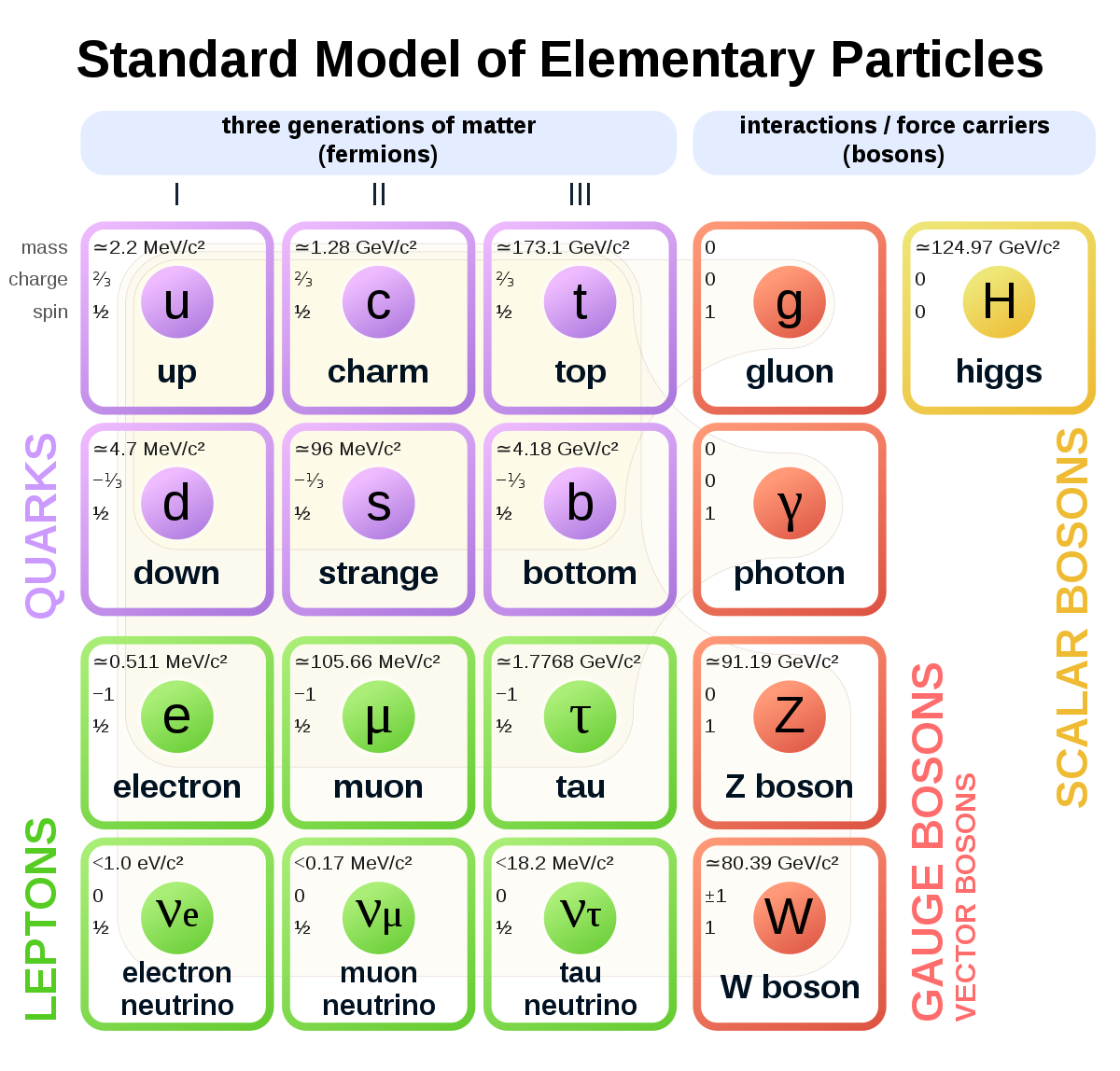

Topic 7 Problems

1. The activity of a sample containing a radioactive element is 6400 Bq. After 36 minutes the activity is 800 Bq. What is the half-life of the sample?

A. 4 minutes

B. 8 minutes

C. 12 minutes

D. 18 minutes

2. The reaction p + n → p + π0 is impossible. Which conservation law would be violated if the reaction occurred?

A. charge

B. baryon number

C. lepton number

D. strangeness

3. What process does this Feynman diagram represent?

A. electron emitting photon

B. electron absorbing photon

C. positron emitting photon

D. positron absorbing photon

4. A sample contains a small quantity of a radioactive element with a very long half-life. The activity is constant and equal to A. The temperature of the sample is increased. What are the effects if any, on the half-life and activity of the sample?

A.

B.

C.

D.

5. The binding energy per nucleon for about 7 MeV. What is the minimum energy needed to separate thenucleons of ?

A. 7 MeV

B. 35 MeV

C. 42 MeV

D. 77 MeV

6. The atomic line spectra of elements provides evidence for the existence of

A. photons

B. electrons

C. quantized energy states within nuclei

D. quantized energy states within atoms

7. Which of the following best describes why alpha-particles travel only a short distance in air?

A. They undergo radioactive decay

B. They undergo elastic collisions with air molecules

C. They ionize air molecules

D. They are attracted by the nuclei of air molecules

8. When the isotope aluminium-27 is bombarded with alpha particles, the following nuclear reaction can take place. Which of the following correctly gives the atomic (proton) number and mass (nucleon) number of the nucleus X?

A.

B.

C.

D.

9. The graph below illustrates the variation with nucleon number (mass number) N of the binding energy per nucleon E of nuclei. Which of the labelled nuclei is the most stable?

A.

B.

C.

D.

10. The graph below shows the variation with mass (nucleon) number of the average binding energy per nucleon. Which direction indicates a fission reaction with a release of energy?

A. I

B. II

C. III

D. IV

Number of correct answers: