Jump to: Circular motion 6.1 Newton’s law of gravitation 6.2 Topic 6 problems

6.1 Circular motion

Period, frequency, angular displacement and angular velocity

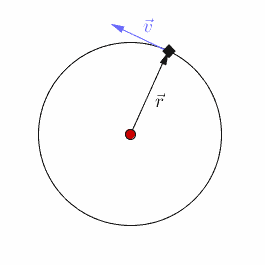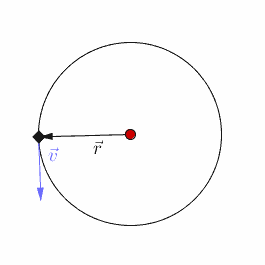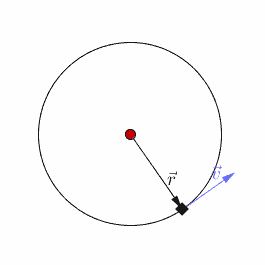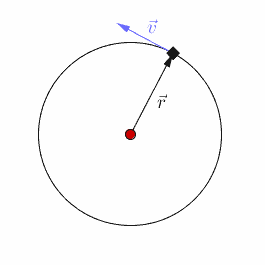
Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed. For example, any point on a propeller spinning at a constant rate is executing uniform circular motion.

While the magnitude of its velocity remains constant, the direction of its velocity is constantly changing.The acceleration causing this change in velocity is always directed towards the center of the circular path.

The period, T, is the time the object takes to make a complete circle. It is measured in seconds.

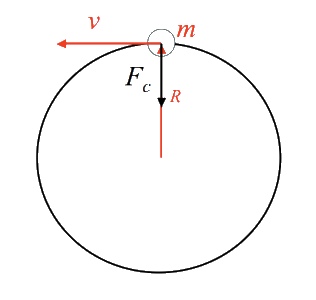
\begin{gather*} v=\frac{2\pi r}{T} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a=\frac{4\pi ^{2} r}{T^{2}} =4\pi ^{2} rf^{2}\\ v=velocity,\ T=period,\ r=radius,\ f=frequency,\ a=acceleration \end{gather*}

Centripetal force

A centripetal force is a net force that acts on an object to keep it moving along a circular path.

The force vector is perpendicular to the velocity vector at each instant. It points towards the center of the circle.

Centripetal force is not a type of force; rather, it is just the name we give to the net force causing a circular motion.

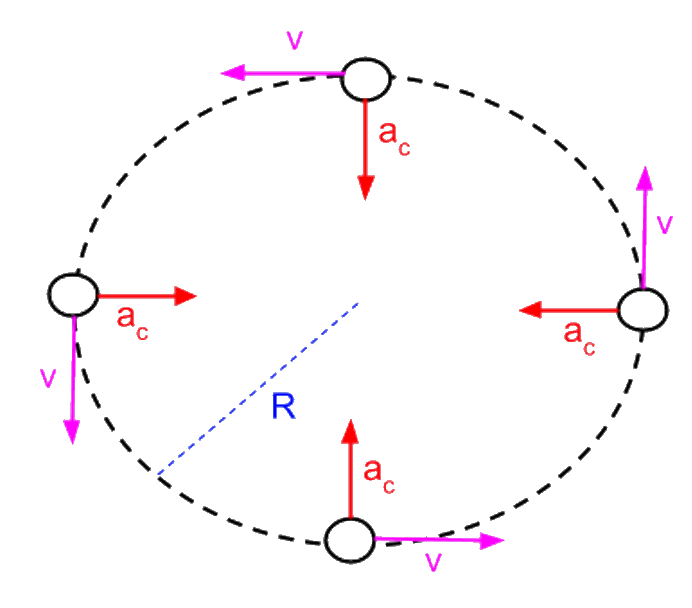
\begin{gather} F_{c} =\frac{mv^{2}}{r}\\ F_{c} =centripetal\ force,\ m=mass,\ v=velocity,\ r=radius\ of\ the\ circle \notag \end{gather}

Centripetal acceleration

In uniform circular motion, the direction of the velocity changes constantly, so there is always an associated acceleration, even though the speed might be constant.

It is directed towards the center of the circular motion and is perpendicular to the instantaneous velocity of the object.

\begin{gather} a=\omega ^{2} r\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a=\frac{v^{2}}{r}\\ a=acceleration,\ \omega =angular\ velocity,\ v=velocity,\ r=radius \notag \end{gather}
Great explanation of circular motion

6.2 Newton’s law of gravitation

Newton’s law of gravitation

\begin{gather} F_{g} =\frac{Gm_{1} m_{2}}{r^{2}}\\ F_{g} =gravitational\ force,\ m=mass\ of\ object,\ r=distance\ between\ the\ center\ of\ the\ object \notag\\ G=gravitational\ constant\ \left( 6.67408\times 10^{-11}\right) \notag \end{gather}

Sir Isaac Newton was an English mathematician and mathematician and physicist who lived from 1642-1727. The legend is that Newton discovered Gravity when he saw a falling apple while thinking about the forces of nature. Whatever really happened, Newton realized that some force must be acting on falling objects like apples because otherwise they would not start moving from rest. Newton also realized that the moon would fly off away from Earth in a straight line tangent to its orbit if some force was not causing it to fall toward the Earth. The moon is only a projectile circling around the Earth under the attraction of Gravity. Newton called this force "gravity" and determined that gravitational forces exist between all objects. Using the idea of Gravity, Newton was able to explain the astronomical observations of Kepler. The work of Galileo, Brahe, Kepler, and Newton proved once and for all that the Earth wasn't the center of the solar system. The Earth, along with all other planets, orbits around the sun. (Stanford)

Video explanation

Gravitational field strenght

Gravitational field strenght at a point is the force per unit mass experienced by a small point mass placed at that point.

\begin{gather} g=\frac{F_{g}}{m}\\ g=gravitational\ field\ strenght,\ F_{g} =gravitational\ force,\ m=mass \notag \end{gather}

g = 9.81ms-2 for Earth

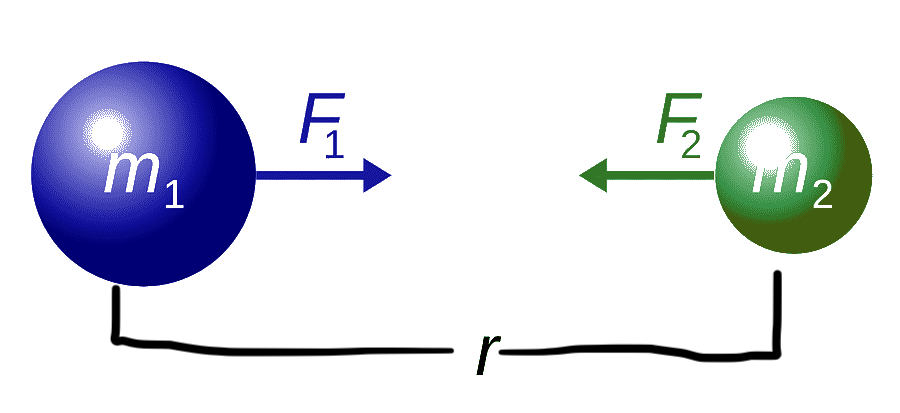
Inverse square law

The gravitational force is always attractive, proportional to 1/r2, and proportional to m.

Laws that depend on 1/r2 are called inverse-square laws.

If the distance between the masses is doubled without changing mass, then the force between masses goes down to a quarter of its original value.

Why gravity is not a force? (optional)
Which way is down? (optional)

Topic 6 Problems

1. A planet has double the mass of Earth and half its radius. What is the gravitational field strength on the surface of this planet?

A. 10Nkg-1

B. 20Nkg-1

C. 40Nkg-1

D. 80Nkg-1

2. A satellite orbits the Earth in a circular orbit. The only force on the satellite is the gravitational force from the Earth. Which of the following is correct about the acceleration of the satellite?

A. It is zero

B. It is constant in magnitude and direction

C. It is constant in magnitude but not in direction

D. It is not constant in magnitude or direction

3. The centripetal force that causes a car to go round a bend in the road is provided by

A. the force produced by the car engine acting on the wheels

B. the friction between the tyres and the road

C. the weight of the car

D. the force exerted by the driver on the steering wheel

4. A particle P is moving in a circle with uniform speed. Which one of the following diagrams correctly shows the direction of the acceleration a and velocity v of the particle at one instant of time?

A.

B.

C.

D.

5. In Newton’s universal law of gravitation the masses are assumed to be

A. extended masses

B. masses of planets

C. point masses

D. spherical masses

6. The acceleration of free fall of a small sphere of mass 5.0 × 10–3 kg when close to the surface of Jupiter is 25 ms–2. The gravitational field strength at the surface of Jupiter is

A. 2.0 × 10–4 N kg–1

B. 1.3 × 10–1 N kg–1

C. 25 N kg–1

D. 5.0 × 103 N kg>–1

7. Gravitational field strength at a point may be defined as

A. the force on a small mass placed at the point

B. the force per unit mass on a small mass placed at the point

C. the work done to move unit mass from infinity to the point

D. the work done per unit mass to move a small mass from infinity to the point

8. Planet X has radius R and mass M. Planet Y has radius 2R and mass 8M. Which one of the following is the correct value of the ratio:
\begin{equation} \frac{gravitational\ field\ strength\ at\ surface\ of\ planet\ X}{gravitational\ field\ strength\ at\ surface\ of\ planet\ Y} \end{equation}

A. 4

B. 2

C. 1/2

D. 1/4

Number of correct answers: