Jump to: Describing fields 10.1 Fields at work 10.2 Topic 10 Problems

10.1 Describing fields

Fields

A field exist when one object is able to exert a force on another object at a distance.

Electric fields Gravitational fields
An electrostatic force exists between charged objects A gravitational force exists between objects
Associated with positive and negative charge A gravitational field is associated with each mass. It acts on other masses in the field
When the two objects have the same charge, the force between them is repulsive. When two objects have opposite charge, the force between them is attractive. Gravity is always an attractive force.

Field strength

Electric fields Gravitational fields
\begin{equation} electric\ field\ strenght=\frac{force\ acting\ on\ a\ positive\ charge}{magnitude\ of\ test\ charge} \end{equation} \begin{equation} gravitational\ field\ strength=\frac{force\ acting\ on\ test\ mass}{magnitude\ of\ test\ mass} \end{equation}
The direction of the field is the same as the direction of the force acting on a positive charge. Gravitational force is always attractive.
Measured in N C-1 Measured in N kg-1

Energy

Electric fields Gravitational fields
Potential difference Potential energy
\begin{gather} V=\frac{W}{Q}\\ V=potential\ difference,\ W=work\ done,\ Q=charge \notag \end{gather} \begin{gather} \Delta E_{P} =mg\Delta h\\ \Delta E_{P} =change\ in\ gravitational\ potential\ energy,m=mass, \notag\\ \Delta h=change\ in\ height,\ g=gravitational\ field\ strenght\ \ \notag \end{gather}
Measured in volts. Applies only when g is relatively constant over the height change.

Field lines - electric fields

Field lines visualise the shape of the electric field that arises from static charges.

The electric field between two parallel plates: is uniform betweeen the plates and becomes weaker at the edges (edge effects).

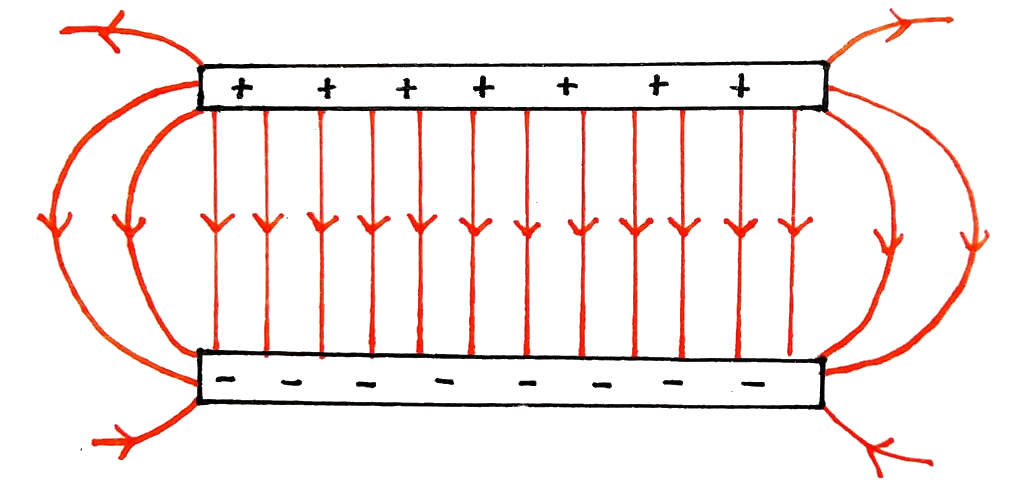
The strenght of the electric field depends on the potential difference between plates.

The lines of equal potential difference between two plates are equipotentials.

Equipotentials: are regions where charges can move without work being done, are cut by field lines at 90°, and are scalars.

Field due to a single point charge (radial field)
Field due to two point charges of the opposite sign
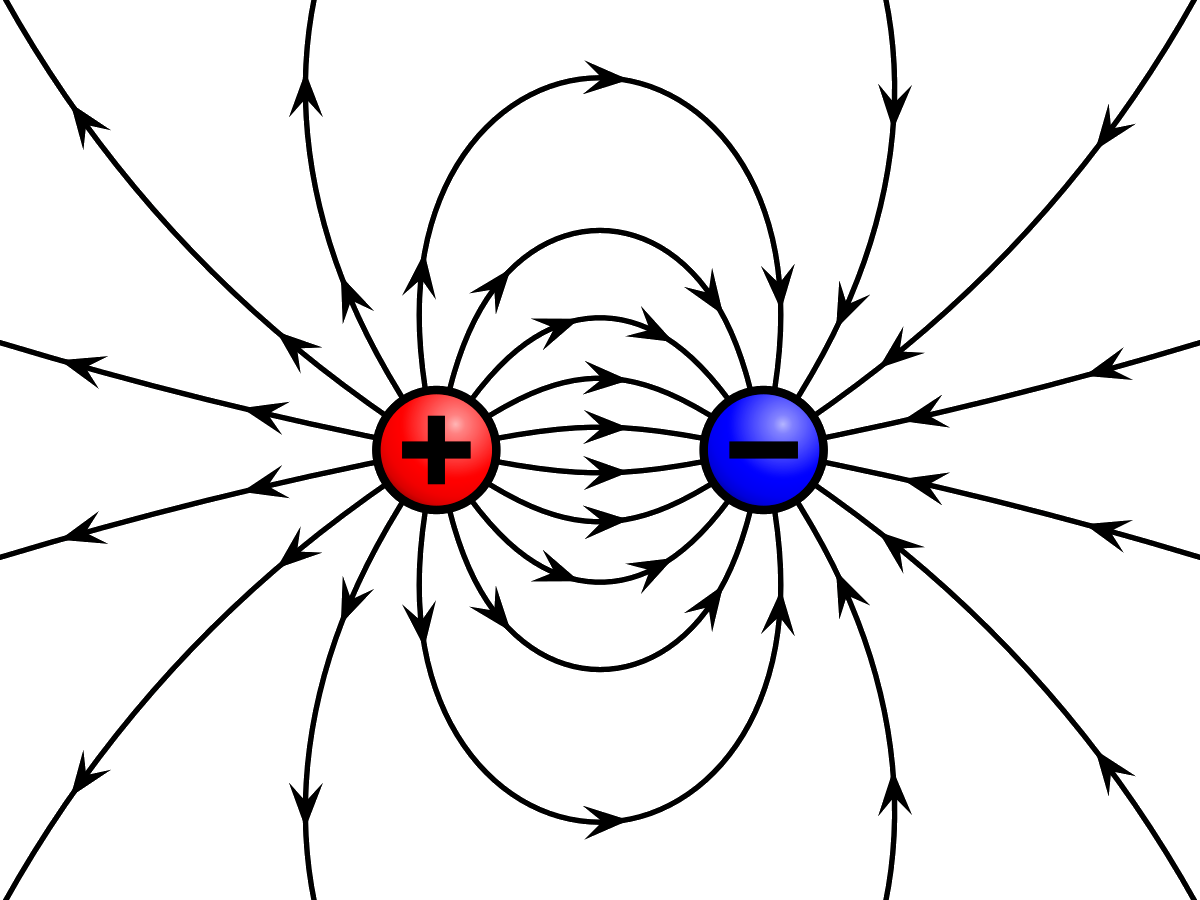
Field between a point charge and a charged plate

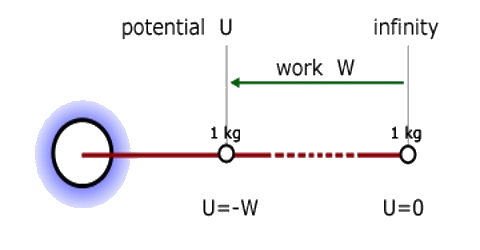
The electric potential at a point is the work done in bringing a unit positive test charge from infinity to the point.

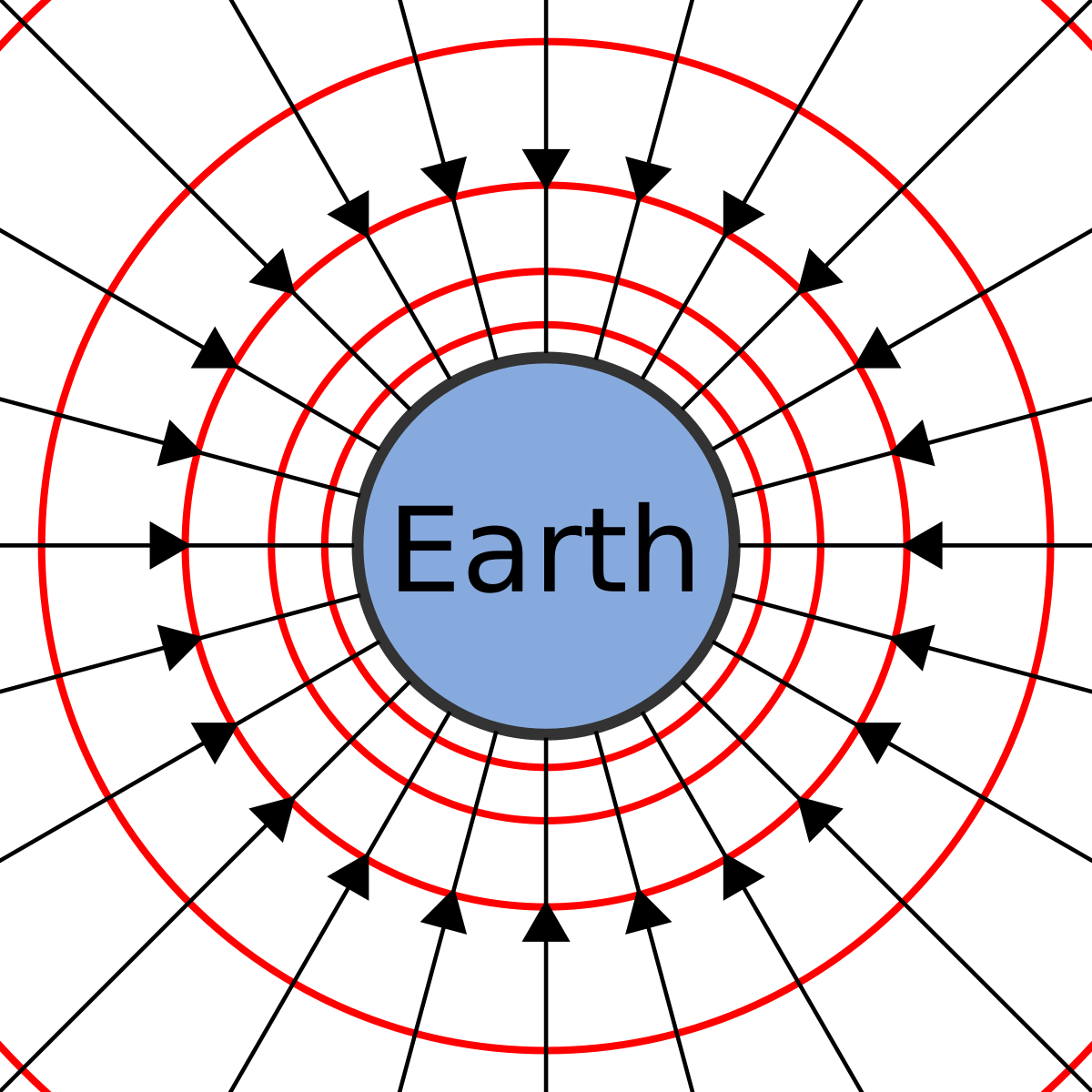
Fields and equipotentials in gravitation

Gravitational fields that surround a point are radial fields.

Gravitational potential difference is the work done in moving a unit mass between two points.

\begin{gather} \Delta V_{g} =\frac{W}{m}\\ \Delta V_{g} =change\ in\ gravitational\ potential,\ W=work\ done,\ \notag\\ m=mass\ of\ the\ object \notag \end{gather}

Gravitational potential is defined to be zero at infinity

\begin{gather} F\varpropto \frac{1}{r^{2}}\\ F=force,\ r=distance \notag\\ \notag\\ Therefore,\ \notag\\ \lim _{r\rightarrow \infty }\frac{1}{r^{2}} =0 \notag \end{gather}

When the distance is very large, the gravitational force decreases to 0.

Gravitational potential at a point is defined to be work done per unit mass in moving a test mass from infinity to the point.

Gravitational & Electric Fields - video explanation

10.2 Fields at work

Forces and inverse-square law behaviour

Both fields obey an inverse-square law, where the force between the objects is inversely proportional to the distance between them squared.

Electric fields Gravitational fields
\begin{gather} F_{E} =+\frac{kq_{1} q_{2}}{r^{2}}\\ F_{E} \ =\ force\ between\ the\ point\ charges,\ r=distance\ between\ them \notag\\ k=\frac{1}{4\pi \epsilon _{0}} \notag\\ \epsilon _{0} =permittivity\ of\ free\ space\ or\ the\ medium\ \notag \end{gather} \begin{gather} F_{g} =\frac{Gm_{1} m_{2}}{r^{2}}\\ F_{g} \ =\ force\ between\ the\ point\ masses,m=mass\ \notag\\ r=distance\ between\ them \notag\\ \notag \end{gather}
The sign of the overall result indicates the direction of the force. Negative indicates attraction, positive indicates repulsion. The value of G is a universal constant

Electric field strenght and potential gradient

For a uniform field between parallel plates:

\begin{gather} E=\frac{V}{d} =\frac{F}{Q}\\ \notag\\ E=electric\ field\ strenght,\ V=potential\ difference\ between\ plates \notag\\ d=distance,\ F=force\ that\ acts\ on\ the\ charge,\ Q=charge \notag\\ \notag \end{gather}
Electric charge, field, and potential - Khan Academy

Electric field strength and surface charge density

\begin{gather} \frac{Q}{A} =\epsilon _{0}\frac{V}{d}\\ Q=charge,\ A=area,\ \epsilon _{0} =permittivity,\ d=distance \notag \end{gather}

Therefore,

\begin{gather} \frac{Q}{A} =\sigma \\ \sigma =surface\ charge\ density \notag \end{gather}

Thus between the plates:

\begin{gather} E=\frac{\sigma }{\epsilon _{0}}\\ E=electric\ field\ strenght,\ \sigma =surface\ charge\ density,\ \notag\\ \epsilon _{0} =permittivity \notag \end{gather}

For surface of any conductor (singular):

\begin{gather} E=\frac{\sigma }{2\epsilon _{0}}\\ E=electric\ field\ strenght,\ \sigma =surface\ charge\ density,\ \notag\\ \epsilon _{0} =permittivity \notag \end{gather}

Graphical interpretations of electric field strength and potential

\begin{gather} E=-potential\ gradient=-\frac{\Delta V_{e}}{\Delta x}\\ E=electric\ field\ strenght,\ \Delta V_{e} =variation\ of\ the\ potential \notag\\ \Delta x=change\ in\ distance \notag \end{gather}

The minus sign means that the direction of the electric field is opposite the variation of potential of a positive charge.

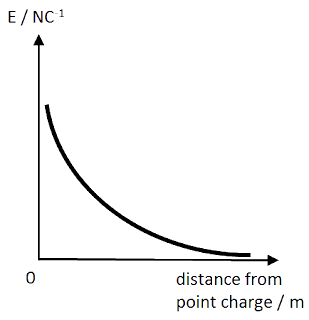
\begin{gather} V_{e} =\frac{Q}{4\pi \epsilon _{0} r}\\ V_{e} =electric\ potential,\ \epsilon _{0} =permittivity,\ r=distance\ from\ point\ charge \notag\\ Q=charge\ creating\ the\ field \notag \end{gather}

If charge q is in a field that arises from another single point charge Q:

\begin{gather} E_{ \begin{array}{l} p\\ \end{array}} =\frac{kqQ}{r} =\frac{qQ}{4\pi \epsilon _{0} r}\\ E_{ \begin{array}{l} p\\ \end{array}} =potential\ energy,\ r=distance\ between\ charges \notag\\ \notag \end{gather}

Example:

A point charge has a magnitude of -0.48 nC. Calculate the potential 1.5m from this charge.

\begin{gather} V_{e} =\frac{Q}{4\pi \epsilon _{0} r}\\ \notag\\ V_{e} =\frac{-0.48\ *\ 10-9}{4\pi \epsilon _{0} *\ 1.5} =2.9\ V \notag \end{gather}

Potential inside a hollow conducting charged sphere

Outside a charged conducting sphere, the potential is indistinguishable from that of a point charge. This is because the field lines leave the surface of the sphere at 90°, therefore they are radial.

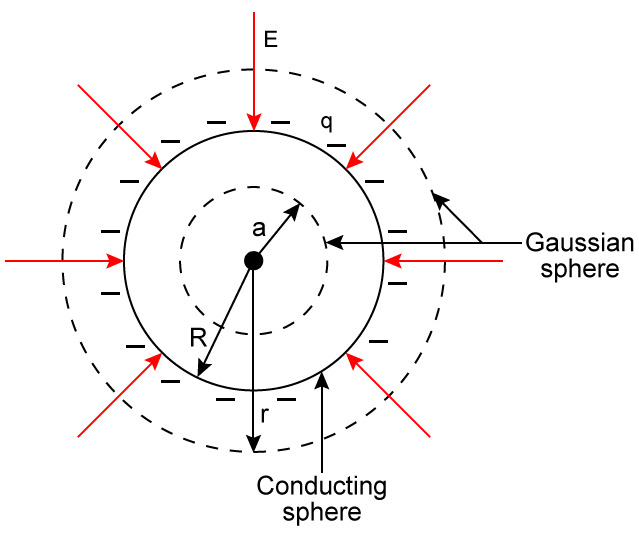
The field inside the sphere

The surplus charge must be on the outside of the sphere because the charges will move until they are as far apart as possible, the charges will move until they are all in equilibrium (equidistant from the surface).

Gravitational potential

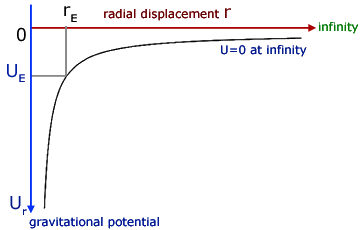
\begin{gather} g=-\frac{\Delta V_{g}}{\Delta r}\\ \notag\\ g=gravitational\ field\ strenght,\ \Delta V_{g} =gravitational\ potential \notag\\ r=distance \notag \end{gather}

For a field due to point mass M with a point mass m at a distance r from it:

\begin{gather} V_{g} =-\frac{Gm}{r}\\ V_{g} =gravitational\ potential,\ G=gravitational\ constant \notag \end{gather}

The potential energy of m at distance r from mass M:

\begin{gather} E_{p} =mV_{g} =-\frac{GMm}{r}\\ \notag \end{gather}

The forces are always attractive for gravity, therefore the potential is always negative with a maximum of zero at infinity (horizontal asymptote).

Gravitational Fields - video explanation

Potential inside a planet

The inner solid sphere (inside the planet) is an Earth with a smaller radius. The gravitational field strenght of that inner sphere is given by:

\begin{gather} g'\ =\frac{G\ *\ reduced\ mass\ of\ Earth}{radius\ of\ small\ Earth^{2}}\\ \notag \end{gather}

The outer shell does not give rise to a gravitational field.

\begin{gather} g'\ =\frac{4\pi G\rho r'\ }{3}\\ \rho =density\ of\ planet,\ r'\ =radius\ of\ the\ inner\ sphere \notag\\ \notag \end{gather}

Orbiting

Linear orbital speed:

\begin{gather} v_{orbit} =\sqrt{\frac{GM}{r}}\\ v_{orbit} =orbital\ velocity,\ M=mass\ of\ planet,\ r=radius\ of\ tbe\ orbit \notag\\ \notag \end{gather}

Orbital period:

\begin{gather} T_{orbit} =\sqrt{\frac{4\pi ^{2} r^{3}}{GM}}\\ v_{orbit} =orbital\ velocity,\ M=mass\ of\ planet,\ r=radius\ of\ tbe\ orbit \notag\\ \notag \end{gather}
Video explanation
Polar orbit

An orbit relatively close to the Earth's surface (100 km). The satellites often orbit over the poles. The linear speed of the satellite is about 7800 ms-1.

Geosynchronous satellites

They orbit at large distances above the Earth. The orbital period is around 24 hours, so they can be made to stay in the same area of the sky, following a figure-eight orbit.

Geostationary orbit

It is a special kind of geosynchronous orbit that orbits above the Equator and will seem stationary when viewed from the surface. They are used for communication purposes and collecting images weather forecasts.

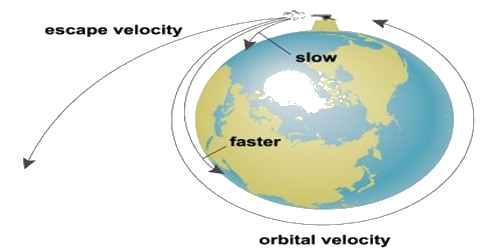
Classes of orbits - video

Escape velocity

Escape velocity is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a massive body, that is, to achieve an infinite distance from it.

\begin{gather} v_{e} =\sqrt{\frac{2GM}{r}}\\ r=distance\ from\ the\ center\ of\ the\ mass,\ v_{e} =escape\ velocity \notag\\ M=\ mass\ of\ the\ body\ to\ be\ escaped\ from \notag\\ \notag \end{gather}

Escape velocity is roughly 12000 ms-1 for Earth.

Escape velocity - video explanation

Charges moving in magnetic fields

In a magnetic field the force is always at right angles to the motion of the electron (Fleming's left hand rule) and so the resulting path of the electron is circular.

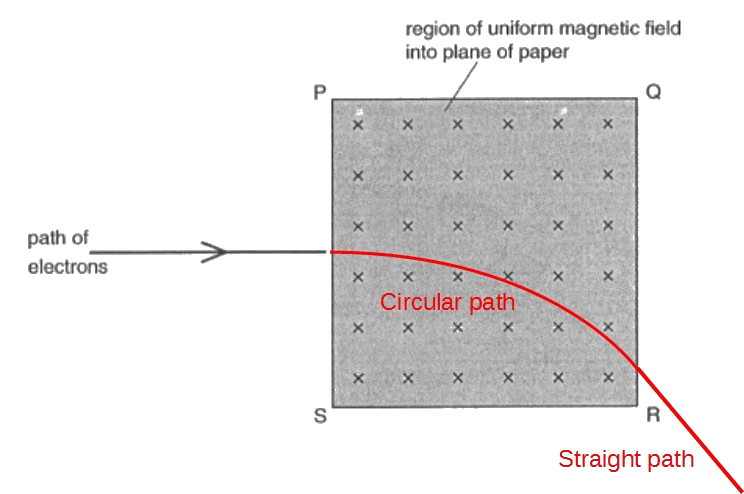
Force acting on electron:

\begin{gather} \frac{m_{e} v^{2}}{r} =Bqv\\ \notag\\ m_{e} =mass\ of\ electron\ \left( 9.1\ x\ 10^{-31}\right) ,\ q=charge \notag\\ v=speed,\ r=radius\ of\ circular\ orbit,\ B=magnetic\ field\ strenght \notag \end{gather}

Radius of the circle due to centripetal force:

\begin{gather} r=\frac{m_{e} v}{Bq} =\frac{p}{Bq} =\frac{\sqrt{2m_{e} E_{k}}}{Bq}\\ \notag\\ m_{e} =mass\ of\ electron\ \left( 9.1\ x\ 10^{-31}\right) ,\ q=charge \notag\\ v=speed,\ r=radius\ of\ circular\ orbit,\ B=magnetic\ field\ strenght \notag\\ p=momentum \notag \end{gather}
Electrons In A Uniform Magnetic Field - video
Motion in a magnetic field - video

Charges moving in electric fields

Electron follows a parabolic path.

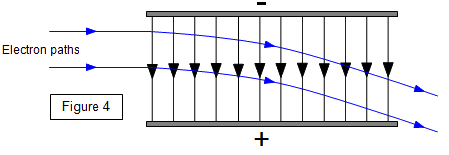Electron moving in a uniform field

Charges moving in magnetic and electric fields

Combining electric and magnetic fields at right angles to each other:

\begin{gather} F_{E} =F_{B} \ \\ \notag\\ Thus:\ \notag\\ qE=Bqv \notag\\ q=charge,\ E=electric\ field\ strength,\ B=magnetic\ field\ strength,\ v=speed \notag\\ \notag\\ Leading\ to: \notag\\ v=\frac{E}{B} \notag \end{gather}

There is some speed where the forces are balanced. This arrangement is a velocity selector.

Bainbridge mass spectrometer - video

Topic 10 Problems

1. Four charges that are equal in magnitude are put at the vertices of a square, as shown in the diagram.

A. Along the y-axis

B. Along the x-axis

C. At the origin only

D. Along both axes

2. Consider two spherical masses, each of mass M, whose centres are a distance d apart. Which of the following is true at the point midway on the line joining the two centres?

A.

B.

C.

D.

3. Two identical solid steel spheres touch. The gravitational force between them is F. The spheres are now replaced by two touching solid steel spheres of double the radius. What is the force between the spheres now?

A. 4F

B. F/4

C. F/16

D. 16F

4. Shown are four arrangements of two unequal positive point charges separated by various distances. Which two arrangements result in the same electric potential energy?

A. I and II

B. II and IV

C. III and IV

D. I and III

5. The figure shows two oppositely charged parallel plates a distance d apart. A proton is launched from the negative plate with initial speed u. The proton just reaches the positive plate. Which graph represents the variation of the speed v of the proton with distance x from the negative plate?

A.

B.

C.

D.

6. The escape speed from a planet is defined as the speed at which an object must leave the planet’s surface to

A. escape completely from the gravitational field of the planet

B. enter a geostationary orbit about the planet

C. escape from the atmosphere of the planet

D. overcome the gravitational force of the planet

7. A satellite is in orbit about Earth. The satellite moves to an orbit closer to Earth. Which of the following correctly gives the change in the potential energy and the kinetic energy of the satellite?

A.

B.

C.

D.

8. A spacecraft orbits Earth. An astronaut inside the spacecraft feels “weightless” because

A. the gravitational field in the spacecraft is negligible

B. the Earth exerts equal forces on the spacecraft and the astronaut

C. the spacecraft and the astronaut have the same acceleration towards the Earth

D. the spacecraft and the astronaut exert equal and opposite forces on each other

9. An isolated conducting sphere of radius r is positively charged. Which one of the following graphs best shows the variation with distance x from the centre of the sphere of the electric potential V?

A.

B.

C.

D.

10. A planet has double the mass of the Earth and double the radius. The gravitational potential at the surface of the Earth is V and the magnitude of the gravitational field strength is g. The gravitational potential and gravitational field strength on the surface of the planet are:

A.

B.

C.

D.

Number of correct answers: