Topic 11

11.1 Electromagnetic induction

Inducing and electromagnetic field

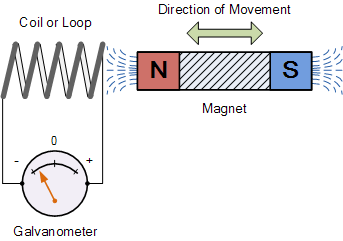
Electromagnetic Induction is a current produced because of voltage production (electromotive force) due to a changing magnetic field.

Electromagnetic Induction was first discovered way back in the 1830s by Michael Faraday.

Lenz's law

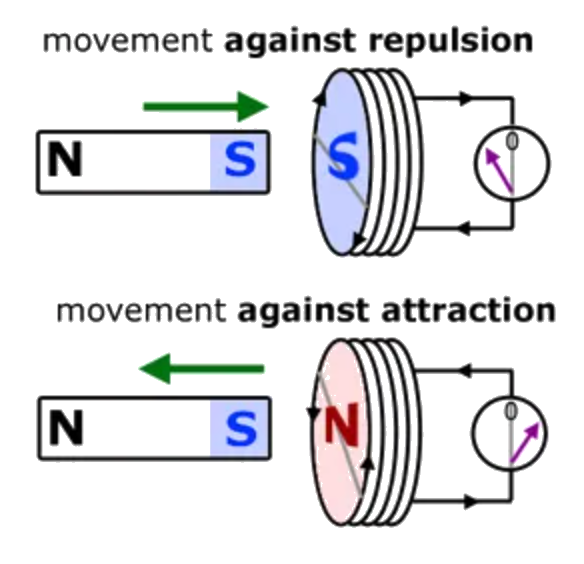
The direction of the induced current is such as to oppose the change that created the current.

Formulated based on the conservation of energy.

Video explanation
Video explanation #2

Magnetic flux and flux density

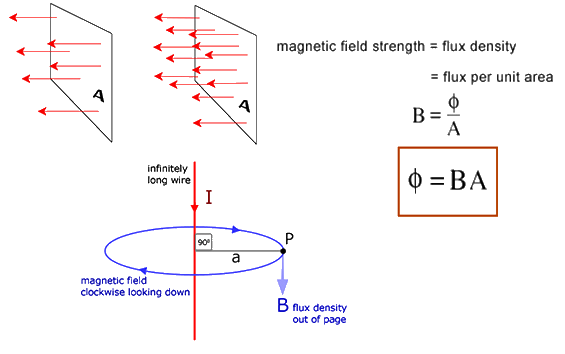
\begin{gather} \epsilon =Blv\\ \epsilon =induced\ emf,\ B=magnetic\ field\ strenght \notag\\ l=lenght\ of\ the\ rod,\ v=speed\ of\ the\ rod \notag \end{gather}

Magnetic flux is a measurement of the total magnetic field which passes through a given area. It is measured in Webers (Wb).

A rate of change of flux of one weber per second induces an emf of one volt across a conductor.

\begin{gather} \Phi =BAcos\theta \\ \Phi =magnetic\ flux,\ B=magnetic\ field,\ A=area, \notag\\ \ \theta =angle\ between\ a\ perpendicular\ vector\ to\ the\ area\ and\ the\ magnetic\ field \notag \end{gather}

The magnetic field strenght is numerically equivalent to magnetic flux density.

Magnetic flux density is measured in weber meter^-2, which is equivalent to one Tesla.

Video explanation

Magnetic flux linkage

Magnetic flux linkage:

\begin{gather} magnetic\ flux\ linkage=N\Phi \\ N=number\ of\ turns\ on\ the\ coil,\ \Phi =magnetic\ flux \notag\\ \notag \end{gather}

Faraday's law:

The induced emf in a circuit is equal to the rate of change of magnetic flux linkage through the circuit.

\begin{gather} \epsilon =-\frac{N\Delta \Phi }{\Delta t}\\ \epsilon =induced\ emf,\ \Delta \Phi =change\ in\ magnetic\ flux,\ \notag\\ N=number\ of\ turns\ in\ coil,\ \Delta t=change\ in\ time \notag\\ \notag \end{gather}

Negative sign added to account for Lenz's law.

Faraday's law introduction
Michael Faraday's biography (optional)

Changing fields and moving coils

Emf can be induced when:

- a wire of coil moves in an unchanging magnetic field

- the magnetic field can change in strenght

- a coil can change its size and orientation in a constant magnetic field

- a combination of the above

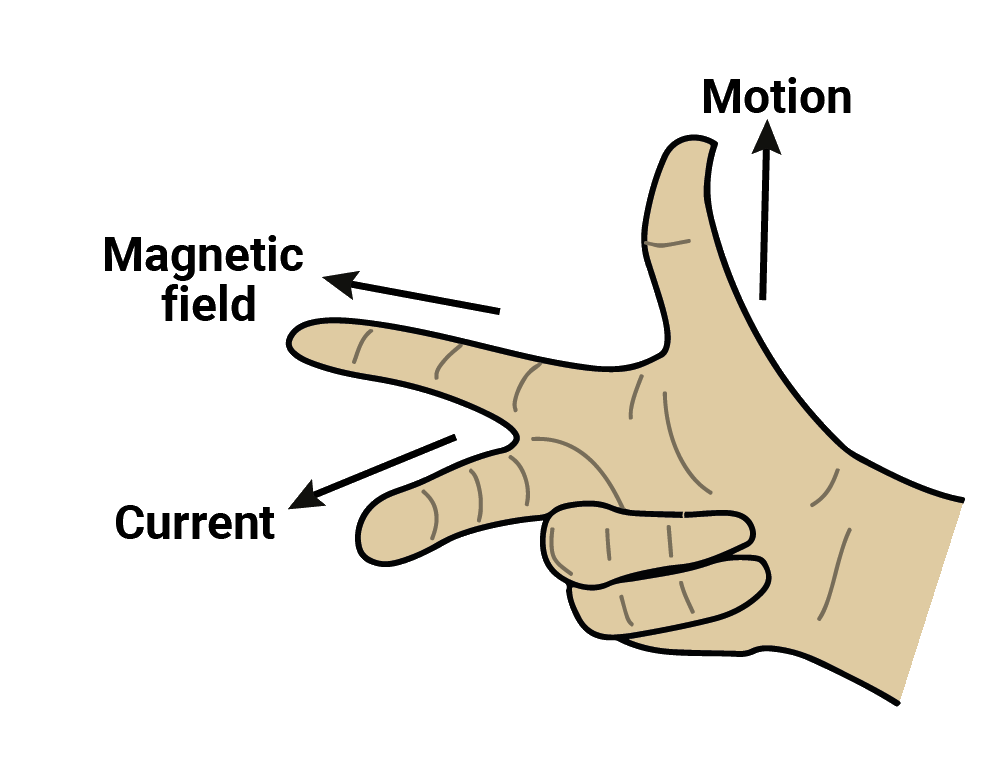
Straight wire moving in a uniform field

The induced emf:

\begin{gather} \epsilon =Bvl\\ \epsilon =induced\ emf,\ B=magnetic\ field\ strength \notag\\ l=lenght\ of\ rod,\ v=speed\ of\ rod \notag \end{gather}

Coil moving

For a coil moving from a position of flux Φ to position of flux 0:

\begin{gather} \epsilon =\frac{N\Phi }{time\ taken\ for\ change}\\ \epsilon =induced\ emf,\ \Phi =magnetic\ flux,\ \notag\\ N=number\ of\ turns\ on\ coil \notag \end{gather}

For a coil in a field flipped through 180°:

\begin{gather} \epsilon =\frac{2N\Phi }{time\ taken\ to\ rotate\ coil}\\ \epsilon =induced\ emf,\ \Phi =magnetic\ flux,\ \notag\\ N=number\ of\ turns\ on\ coil \notag \end{gather}

Magnetic field changes

\begin{gather} \epsilon =-\frac{N\Delta \Phi }{\Delta t}\\ Becomes: \notag\\ \epsilon =-NA\frac{\Delta B}{\Delta t} \notag\\ A=area\ bounded\ by\ the\ coil,\ N=number\ of\ turns, \notag\\ \Delta t=change\ in\ time,\ \Delta B=change\ in\ magnetic\ field\ strength \notag \end{gather}

Video explanation

11.2 Power generation and transmission

Alternating current (AC) generators

AC generator, also known as alternators, is a machine that converts mechanical energy into electrical energy. The generated electrical energy is in the form of an alternating current sinusoidal output waveform. The mechanical energy is usually supplied by steam turbines, gas turbines and combustion engines.

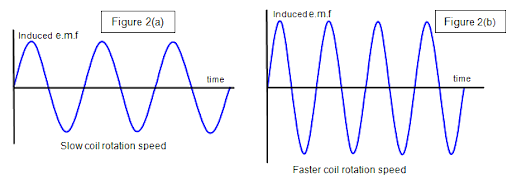
The generated EMF depends on the number of armature coil turns, magnetic field strength, and the speed of the rotating field.

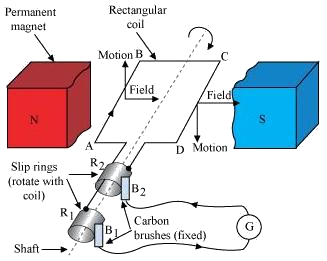
Requirements for an AC generator:

- a rotating coil

- a magnetic field

- movement between the coil and the magnetic field

If the rotation is at constant speed, the induced emf is sinusoidal:

Video explanation

Measuring alternating currents and voltages

The power-time graph is always positive.

The power graph cycles at double the frequency of the current.

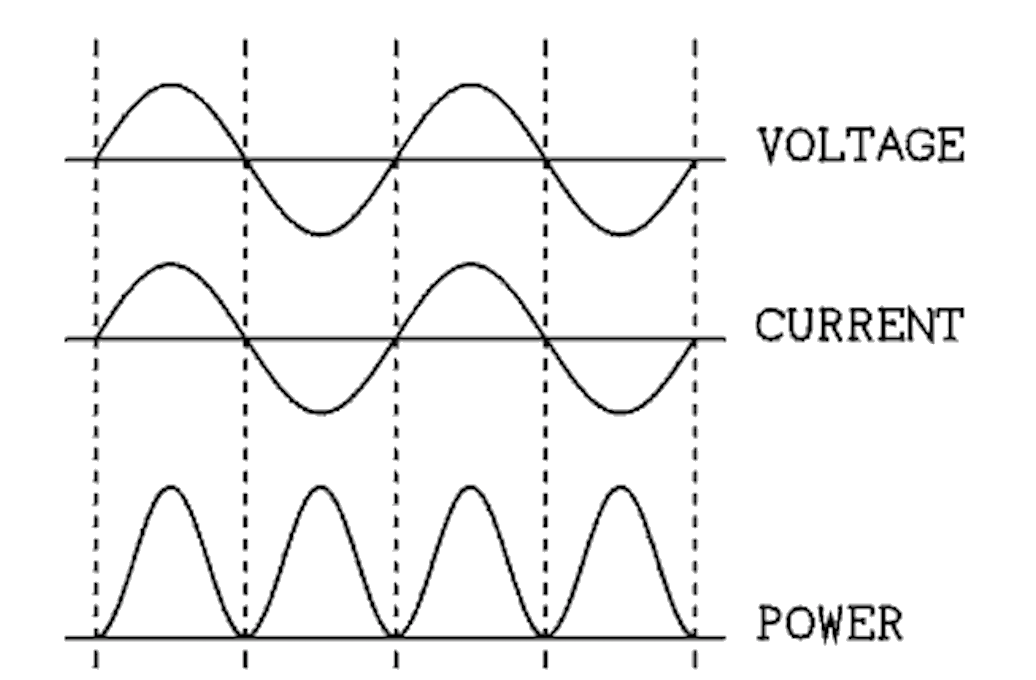
Root mean square (RMS) current:

\begin{gather} I_{rms} =\frac{I_{max}}{\sqrt{2}}\\ I_{max} =peak\ value\ of\ the\ current,\ I_{rms} =RMS\ current \notag\\ \notag\\ V_{rms} =\frac{V_{max}}{\sqrt{2}} \notag\\ V_{rms} =RMS\ voltage,\ V_{max} =peak\ value\ of\ voltage \notag \end{gather}

RMS current value can also be defined as the value of the direct current that dissipates the same power in a resistor.

Video explanation

Transformers

A Transformer is a static electrical machine which transfers AC electrical power from one circuit to the other circuit at the constant frequency, but the voltage level can be altered that means voltage can be increased or decreased according to the requirement.

A transformer consists of:

- an input (primary) coil

- an output (secondary) coil

- an iron core on which the coils are wound

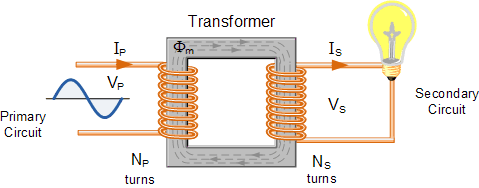
AC current is supplied to the primary coil. A magnetic field is produced by the current in the primary coil. The magnetic field alternates, as the current is alternating. Induced EMF appears in the secondary coil. Energy is transferred from the primary to the secondary coil.

How does a Transformer work?

Transformer rule:

\begin{gather} \frac{\epsilon _{p}}{\epsilon _{s}} =\frac{V_{p}}{V_{s}} =\frac{N_{p}}{N_{s}} \notag\\ \epsilon _{p} =primary\ emf,\ \epsilon _{s} =secondary\ emf \notag\\ V_{p} =primary\ voltage,\ V_{s} =secondary\ voltage \notag\\ N_{p} =primary\ number\ of\ turns,\ N_{s} =secondary\ number\ of\ turns \notag \end{gather}

Step-up transformer (output voltage greater than input voltage):

\begin{equation} N_{s} >N_{p} \end{equation}

Step-down transformer (output voltage less than input voltage):

\begin{equation} N_{s} < N_{p} \end{equation}

Assuming no energy loss:

\begin{gather} I_{p} V_{p} =I_{s} V_{s}\\ \notag\\ I_{p} =current\ in\ primary,\ V_{p} =voltage\ in\ primary \notag\\ I_{s} =current\ in\ secondary,\ V_{s} =voltage\ in\ secondary \notag \end{gather}

Efficiency of a transformer:

\begin{equation} \frac{energy\ supplied\ by\ secondary\ coil}{energy\ supplied\ to\ primary\ coil} \ *\ 100\%=efficiency \end{equation}

Ways to improve efficiency:

- Laminating the core (preventing eddy currents)

- Choosing a 'soft' magnetic material

- Choosing low resistance wire (to prevent heating loss)

- Core design that prevents flux leaking out of the core

Transformer problems
Hard and soft magnetic materials

Transformers in action

Power loss in transmission line:

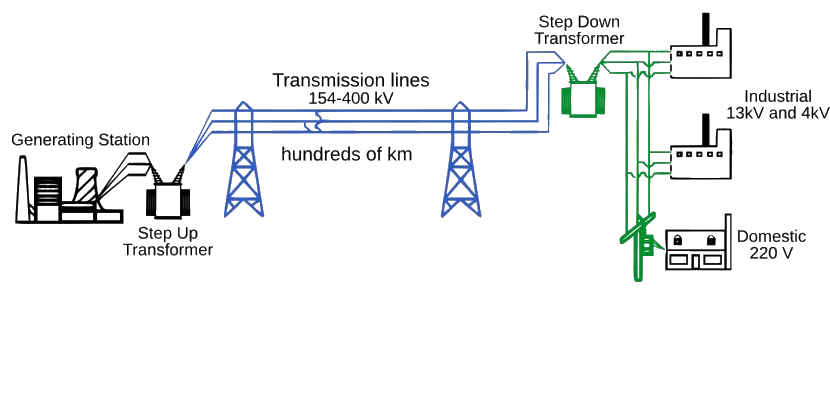\begin{gather} power\ loss=I^{2} R\\ \notag\\ I=current,\ R=resistance \notag \end{gather}

How Do Substations Work?

Rectifying AC

The process of converting AC into DC is called rectification. A device that carries out this process is known as a rectifier.

What is a Rectifier?

Half-wave rectification

A half wave rectifier is defined as a type of rectifier that only allows one half-cycle of an AC voltage waveform to pass, blocking the other half-cycle. Half-wave rectifiers are used to convert AC voltage to DC voltage, and only require a single diode to construct.

Half wave Rectifier Explained

Full-wave rectification

In a Full Wave Rectifier circuit two diodes are now used, one for each half of the cycle. A multiple winding transformer is used whose secondary winding is split equally into two halves with a common centre tapped connection, (C). This configuration results in each diode conducting in turn when its anode terminal is positive with respect to the transformer centre point C producing an output during both half-cycles, twice that for the half wave rectifier so it is 100% efficient as shown below.

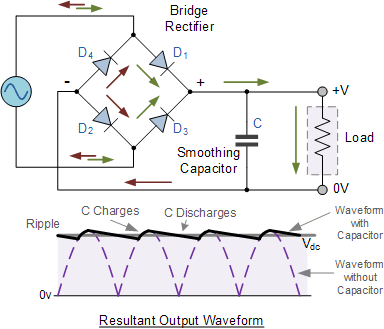Full wave Rectifier Explained

Wheatstone and Wien bridge circuits

The four-diode rectifier arrangement is one of a class of circuits known as bridge circuits

The Wheatstone bridge is used to estimate the resistance of an unknown resistor.

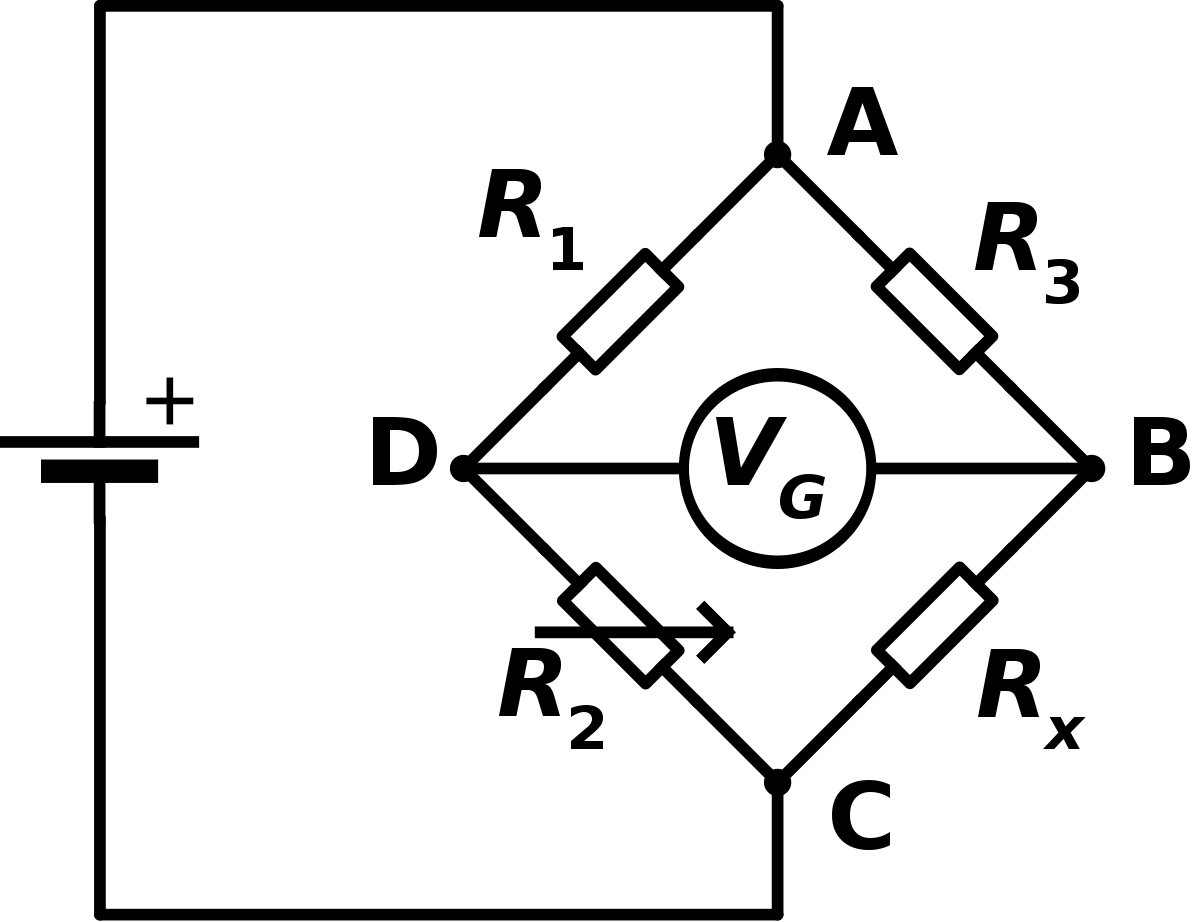
\begin{equation} R_{X} =\frac{R_{1} \times R_{3}}{R_{2}} \end{equation}

Video explanation
Problems video

The Wien bridge circuit is a modified Wheatstone arrangement that allows to see unknown resistance and unknown capacitance. It uses AC supply.

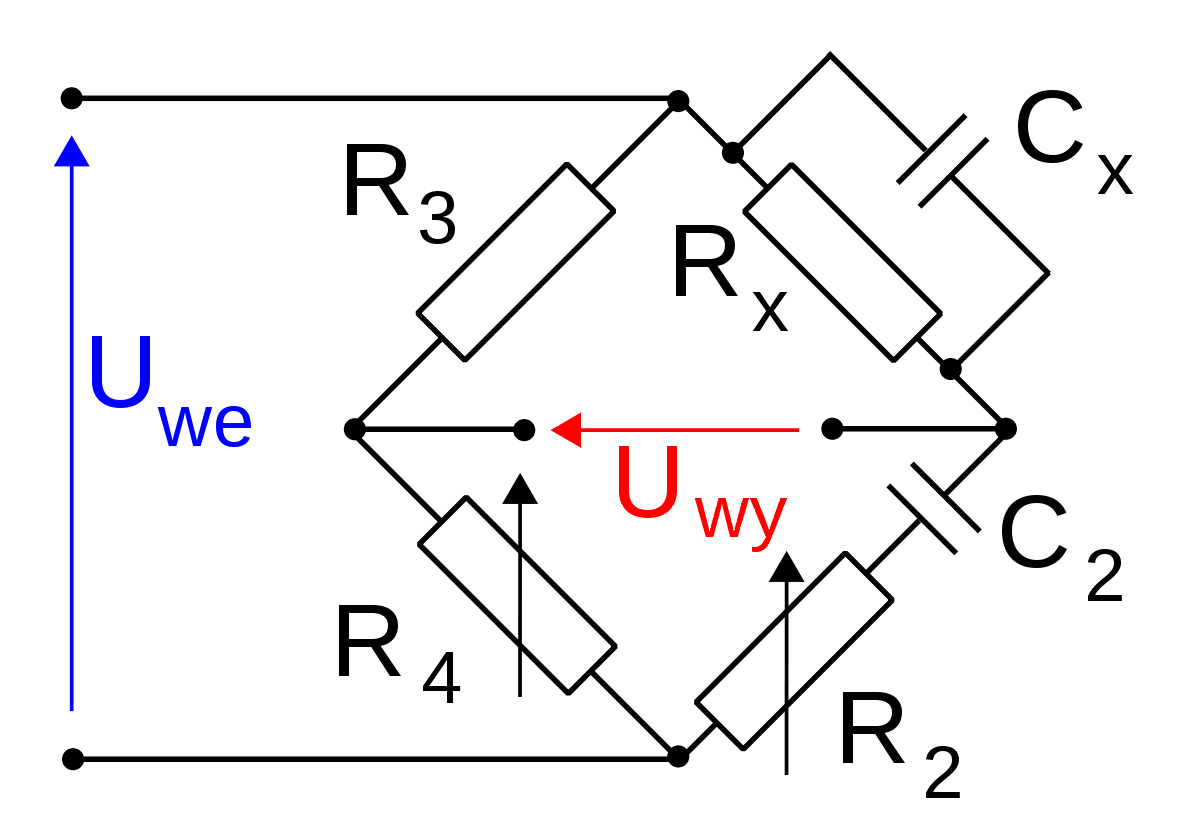
11.3 Capacitance

Capacitors in theory

A capacitor is a device that stores electrical energy in an electric field.

It is the arrangement of parallel plates separated by an insulator.

Capacitance is measured in Farads (F), which is coulomb per volt.

\begin{gather} capacitance\ ( C) =\frac{charge\ stored\ on\ one\ plate}{potential\ difference\ between\ plates} =\frac{Q}{V}\\ \notag\\ Q=charge\ on\ capacitor,\ V=potential\ difference \notag \end{gather}

Video explanation

Energy stored in a capacitor

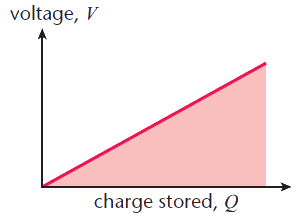
The area under the curve is the energy stored in the capacitor

\begin{gather} Energy\ stored\ =\frac{1}{2} QV=\frac{1}{2}\frac{Q^{2}}{C} =\frac{1}{2} CV^{2}\\ \notag\\ Q=charge\ on\ capacitor,\ V=potential\ difference \notag\\ C=capacitance \notag \end{gather}

Video explanation

Capacitance of a parallel-plate capacitor

When two parallel plates are connected across a battery, the plates are charged and an electric field is established between them, and this setup is known as the parallel plate capacitor.

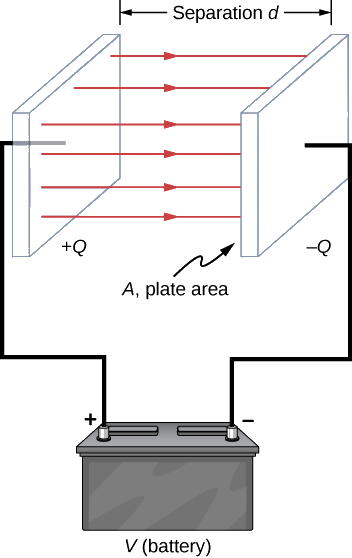
\begin{gather} C=\epsilon \frac{A}{d}\\ C=capacitance,\ d=distance\ between\ plates,\ \epsilon =permittivity \notag\\ A=area\ of\ overlap\ of\ the\ plates \notag \end{gather}

Parallel Plate Capacitor Problems

Capacitors in practice

Ways to increase capacitance of the plates:

- Make the plate overlap area larger

- Position the plates closer together

- Change the value of permittivity

A dielectric is an insulator that is polarized when in an electric field.

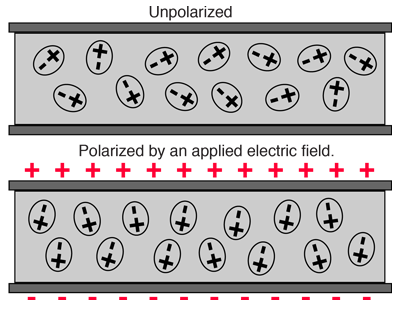
Dielectrics increase the capacitance, as they have increased permittivity than vacuum.

Examples of dielectric materials: paper, mica, Teflon, plastics, ceramics, oxides of some metals.

Relative permittivity chart
Video explanation

Combining capacitors in parallel and series

Another way of changing capacitance values is combining capacitors, in a similar fashion to resistors.

Parallel

When capacitors are connected in parallel, the total capacitance is the sum of the individual capacitors’ capacitances. If two or more capacitors are connected in parallel, the overall effect is that of a single equivalent capacitor having the sum total of the plate areas of the individual capacitors.

\begin{equation} C=C_{1} +C_{2} \end{equation}

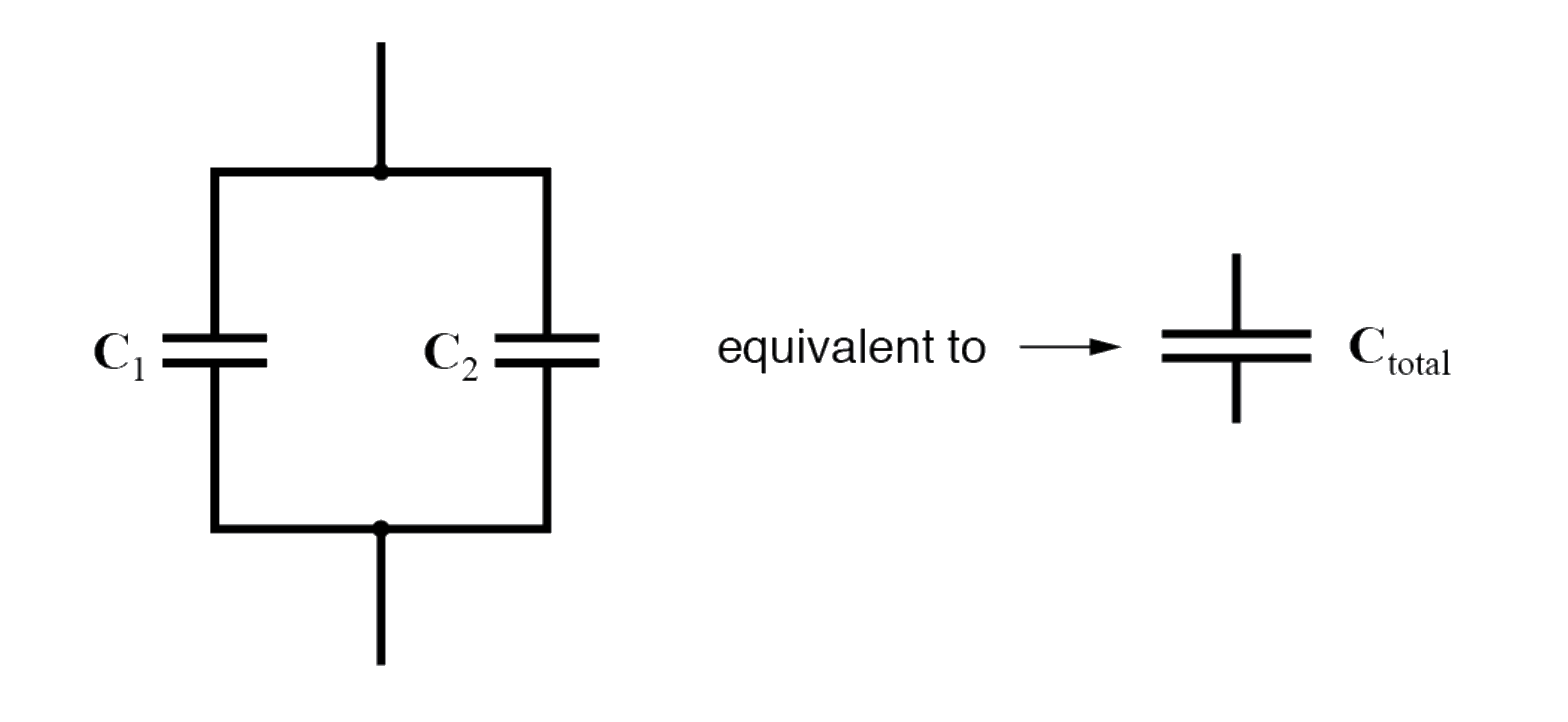
Series

The reciprocal of the total capacitance is equal to the sum of the reciprocals of each capacitance. When capacitors are connected in series, the total capacitance is less than any one of the series capacitors’ individual capacitances.

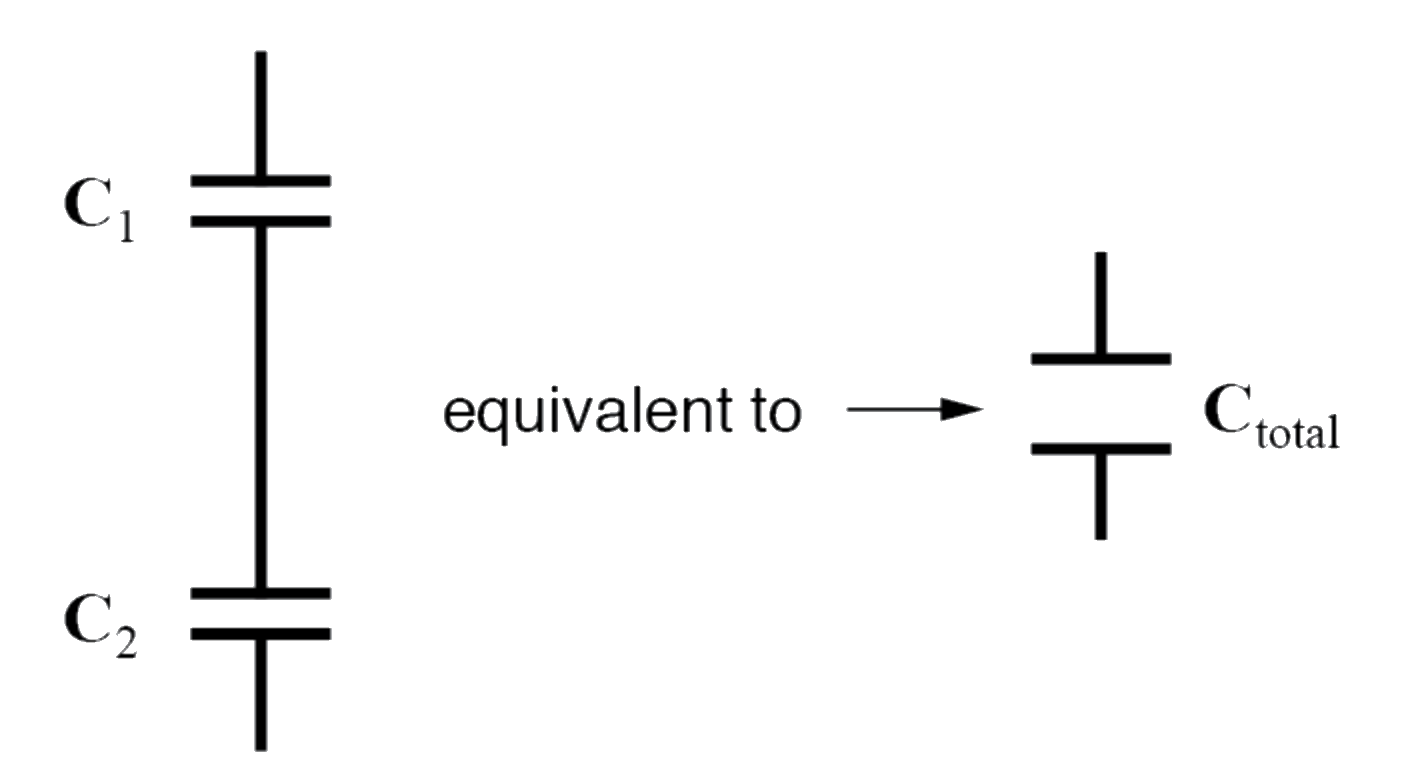
\begin{equation} \frac{1}{C} =\frac{1}{C_{1}} +\frac{1}{C_{2}} \end{equation}

Capacitors in Series and Parallel Explained

Discharging and charging a capacitor

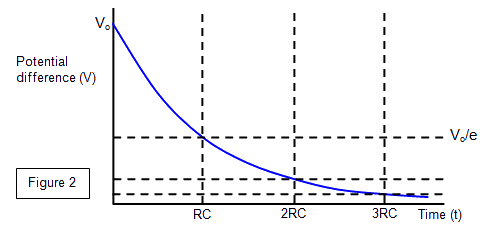
Discharging

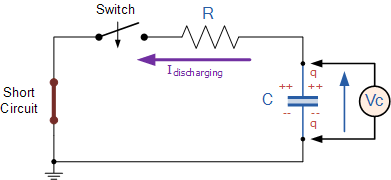
\begin{gather} \Delta Q=-\frac{Q\Delta t}{RC}\\ \Delta t=time\ elapsed\ since\ discharge\ began\ ( negative) ,\ \notag\\ Q=charge,\ \Delta Q=change\ in\ charge,\ R=resistance \notag\\ C=capacitance \notag\\ \notag\\ \Delta Q=-\frac{Q\Delta t}{\tau } \notag\\ \tau =R\times C \notag \end{gather}

Discharging circuit:

Discharge follows a pattern similar to exponential decay

\begin{gather} Q=Q_{0} e^{-\frac{t}{\tau }}\\ \notag \end{gather}

Charging

\begin{gather} \Delta V=\frac{( V_{emf} -V_{c}) \times \Delta t}{RC}\\ \Delta V=change\ in\ potential\ difference,\ R=resistance \notag\\ C=capacitance,\ \Delta t=time\ elapsed\ for\ charging \notag \end{gather}

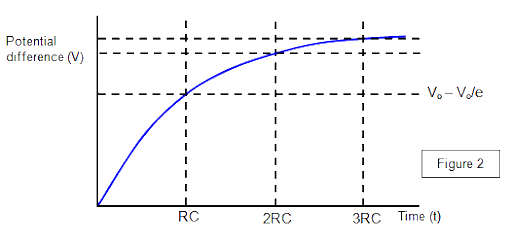Video explanation

11.1 Electromagnetic induction

Inducing and electromagnetic field

Lenz's law

Magnetic flux and flux density

Magnetic flux linkage

Changing fields and moving coils

Straight wire moving in a uniform field

Coil moving

Magnetic field changes

11.2 Power generation and transmission

Alternating current (AC) generators

Measuring alternating currents and voltages

Transformers

Transformers in action

Rectifying AC

Half-wave rectification

Full-wave rectification

Wheatstone and Wien bridge circuits

11.3 Capacitance

Capacitors in theory

Energy stored in a capacitor

Capacitance of a parallel-plate capacitor

Capacitors in practice

Combining capacitors in parallel and series

Parallel

Series

Discharging and charging a capacitor

Discharging

Charging

Topic 11 Problems

1. In which of these circuits can full-wave rectification take place?

2. What will the initial current be in the circuit below the instant the switch is closed, and what will it be eventually a long time after the switch is closed?

3. Capacitor X has capacitance 200 pF and potential difference 100 V. Capacitor Y has capacitance 100 pF and potential difference 200 V. Which row in the table is correct about the energy and charge stored by capacitor Y?

4. The graph shows the variation with time of the power dissipated in a resistor of resistance 2.0 Ω in an ac circuit. What is the rms value of the voltage across the resistor and the period of the current?

5. The variation with time of the current in the primary coil of an ideal transformer is shown below. At which time will the magnitude of the induced emf in the secondary coil be maximum?

6. High voltages are used for the transmission of electric power over long distances because

7. The diagram shows a coil of wire wound on an iron core. When the switch is closed, the ammeter reading gradually increases from zero to a maximum value. What is the explanation for this gradual growth of current?

8. The magnetic flux Φ through a coil having 500 turns varies with time t as shown below. The magnitude of the emf induced in the coil is

9. A capacitor is charged to 6 V and then isolated from the battery. The plates are then pulled apart so their separation is twice as big. The p.d. between the plates will now be

10. A parallel plate capacitor of capacitance 10 pF is charged by connecting to a 6 V battery. Plates are now pushed closer together. Which of the following statements is true