Topic 4

Jump to: Oscillations 4.1 Travelling waves 4.2 Wave characteristics 4.3 Wave behaviour 4.4 Standing waves 4.5 Topic 4 Problems

4.1 Oscillations

Simple harmonic oscillators

Oscillations are periodic motions which center around an equilibrium position.

An object undergoes simple harmonic motion when is experiences a force that is proportional and opposite of the displacement from the equilibrium position.

For example: a pendulum or guitar strings

A simple pendulum

\begin{gather} T=2\pi \sqrt{\frac{L}{g}}\\ T=period,\ L=string\ lenght,\ g=acceleration\ due\ to\ gravity \notag \end{gather}

* mass does not effect the period of the pendulum

A mass-spring system

\begin{gather} T=2\pi \sqrt{\frac{m}{k}}\\ T=period,\ m=mass,\ k=spring\ constant \notag \end{gather}

A mass-spring SHM demonstration

4.2 Travelling waves

Travelling waves

A travelling wave is a disturbance in a medium that is created by a vibrating object and subsequently travels through a medium from one location to another, transporting energy as it moves.

For example, ocean waves

All waves transfer energy but not matter

The direction of a wave is defined by the direction of the energy transfer.

Wavelength, frequency, period and wave speed

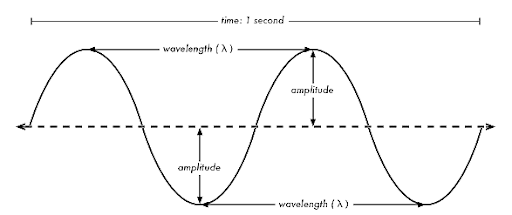
Frequencymeasured in Hertz (Hz) is the number of times the object oscillates per unit time

Periodmeasured in seconds is the time taken for one complete oscillation

\begin{equation} Frequency\ ( f) \ =\frac{1}{Period\ ( T)} \end{equation}

Wave speed

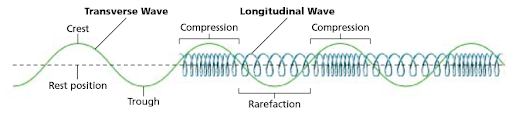
\begin{gather} v=\lambda f\\ v=speed,\ \lambda =wavelenght,\ f=frequency \notag \end{gather}

Transverse and Longitudinal waves

Transverse waves	Longitudinal waves
The direction of oscillation is perpendicular to the direction of the wave	The direction of oscillation is parallel to the direction of the wave
Ocean waves, wave in a guitar string, electromagnetic waves	Sound waves, earthquake P waves
A point with maximum positive displacement is called a crest	A region where particles are closed to each other is called a compression
A point with minimum displacement is called a trough	A region where particles are furthest apart from each other is called a rarefaction

Electromagnetic waves

EM waves travel at the speed of light 3x10⁸ ms^-1

EM waves are transverse waves

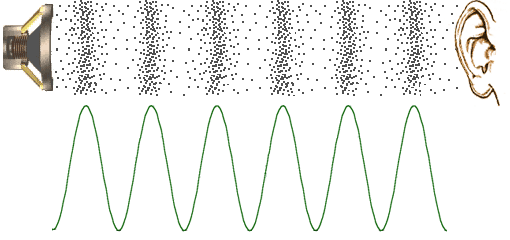
Sound waves

Speed of sound in dry air at 0° Celcius is 331.3 ms^-1

Sound waves are longitudinal waves

4.3 Wave characteristics

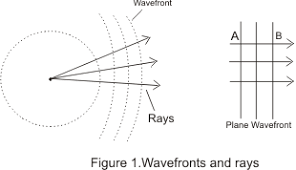
Wavefronts and rays

Wavefronts are lines joining points which vibrate in space (straight or curved). The distance between successive wavefronts is the wavelength of the wave.

Rays are lines which indicate the direction of wave propagation. They are perpendicular to wavefronts.

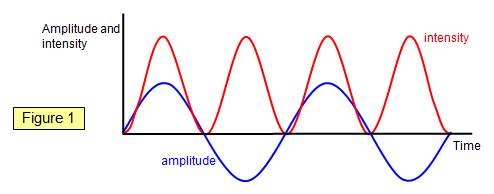
Amplitude and intensity

The amplitude and intensity of a longitudinal wave are related to its energy.

\begin{equation} Intensity\varpropto amplitude^{2} \end{equation}

Superposition

When two or more waves cross at a point, the displacement at that point is equal to the sum of the displacements of the individual waves.

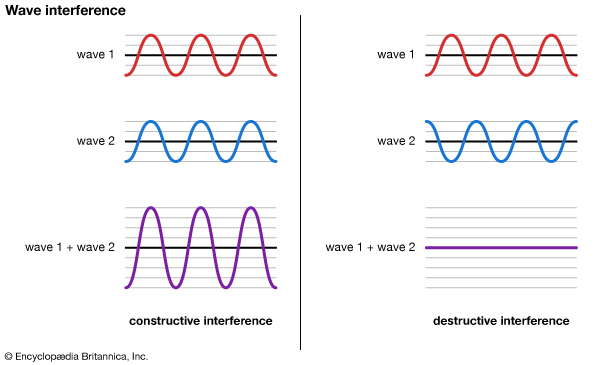
Constructive interference is when two waves add up, as they are in phase

Destructive interference is when two waves cancel out, as they are (in this instance) 180° out of phase

Constructive and destructive interference video explanation

Polarization

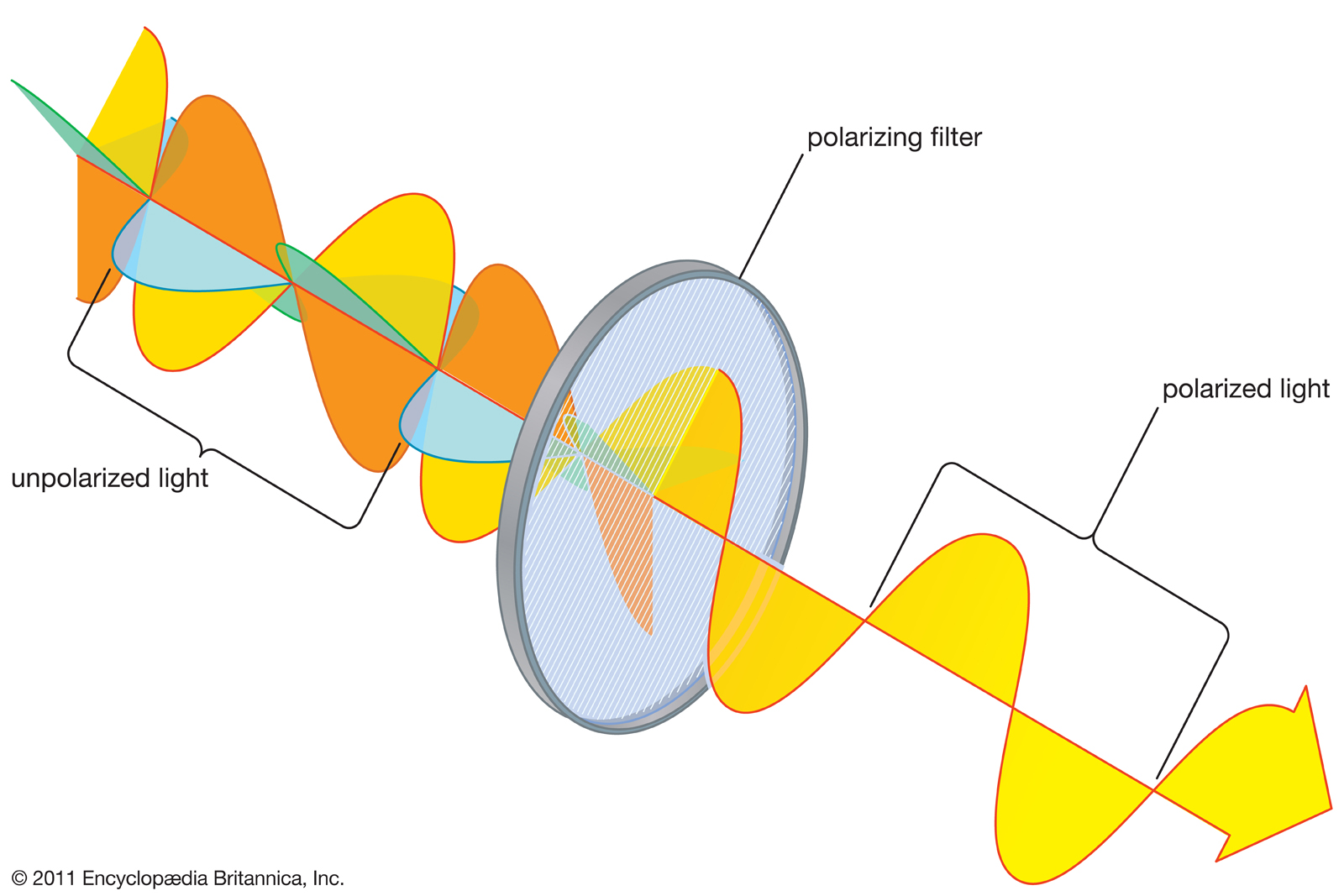
Polarization occurs to light, as it is a transverse wave.

It refers to the orientation of the oscillation of the electric field.

Light is plane polarized if the electric field oscillates in one plane.

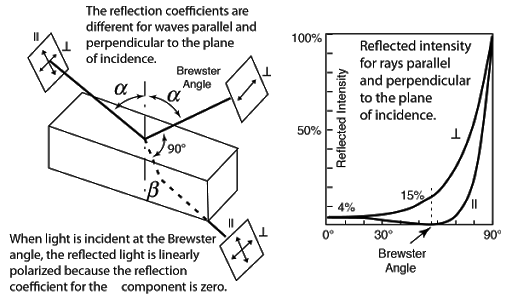
Polarization by reflection

When light is transmitted across a boundary between two mediums with different refractive indexes, part of the light is reflected and the remaining part is refracted.

The reflected light becomes a mixture of polarized and unpolarized light, called partially polarized light.

The extent to which the reflected light is polarized depends on the angle of incidence and the refractive index of the two mediums.

The angle of incidence at which the reflected light is totally polarized is called the Brewster’s angle (ϕ)

\begin{gather} tan( \theta ) =\frac{n_{2}}{n_{1}}\\ n_{1} \ and\ n_{2} \ are\ the\ refractive\ indexes\ \notag \end{gather}

When the angle of incidence is equal to Brewster’s angle, the reflected ray is totally polarized and the reflected ray is perpendicular to the refracted ray.

Polarization Brewster's angle video

Polarizers and Analyzers

Polarizer: a sheet of material polarizing light, when unpolarized light passes through it the intensity of the light is reduced by half.

Analyzer: when polarized light passes through a polarizer, its intensity will be reduced by a factor dependent on the orientation of the polarizer. This property allows us to deduce the polarization of light by using an analyzer.

Malus' law

\begin{gather} I=I_{0} \ cos^{2} \theta \\ \\ I=\ transmitted\ intensity,\ I_{0} =\ initial\ intensity,\ \theta =angle\ between\ the\ light's\ initial\ \notag\\ polarization\ direction\ and\ the\ axis\ of\ the\ polarizer \notag \end{gather}

4.4 Wave behaviour

Reflection and refraction

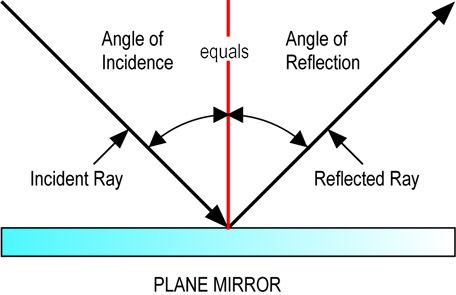
Reflection

Angle of incidence is equal to the angle of reflection

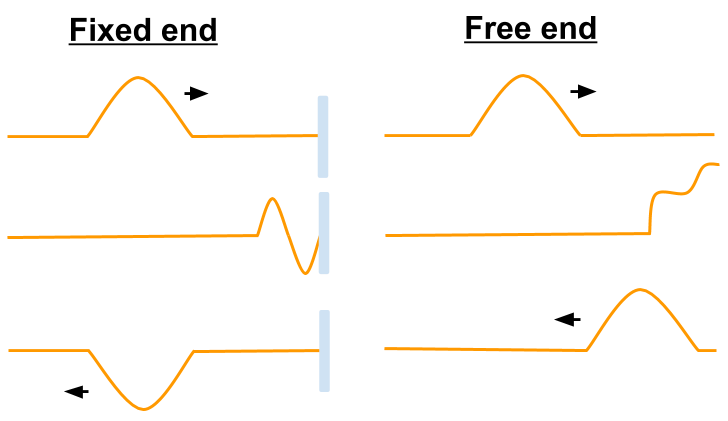
Reflection of waves from a fixed end is inverted. Reflection of waves from a free end is not inverted.

Refraction

Refraction is the change in direction of a wave when it transmits from one medium to another.

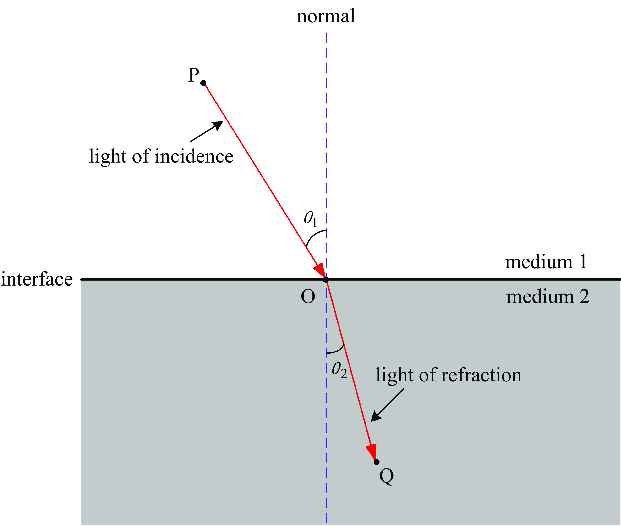
Snell's law

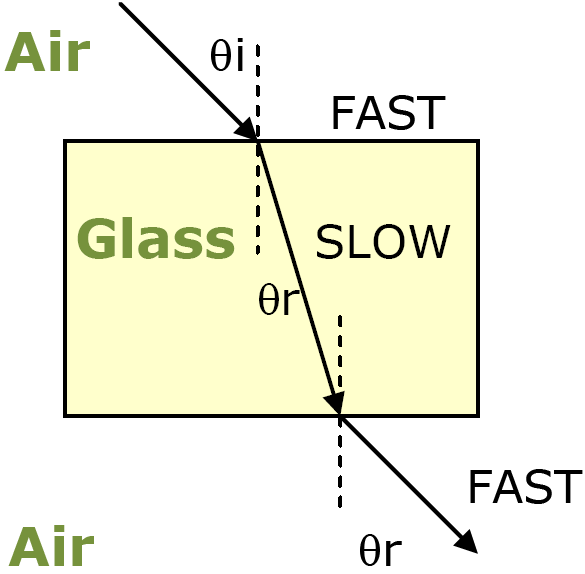
\begin{gather} \frac{n_{1}}{n_{2}} =\frac{sin\theta _{2}}{sin\theta _{1}}\\ \notag\\ \ n_{1} \ and\ n_{2} \ are\ the\ refractive\ indexes\ for\ their\ respective\ mediums,\ \theta \ is\ the\ respective\ angle\ of\ \notag\\ refraction \notag \end{gather}

Furthermore, Snell's law could be expanded to:

\begin{gather} \frac{n_{1}}{n_{2}} =\frac{sin\theta _{2}}{sin\theta _{1}} =\frac{\lambda _{2}}{\lambda _{1}} =\frac{v_{2}}{v_{1}}\\ \notag\\ \lambda \ is\ wavelenght\ and\ v\ is\ speed\ of\ the\ wave \notag \end{gather}

Snell’s law, critical angle and total internal reflection

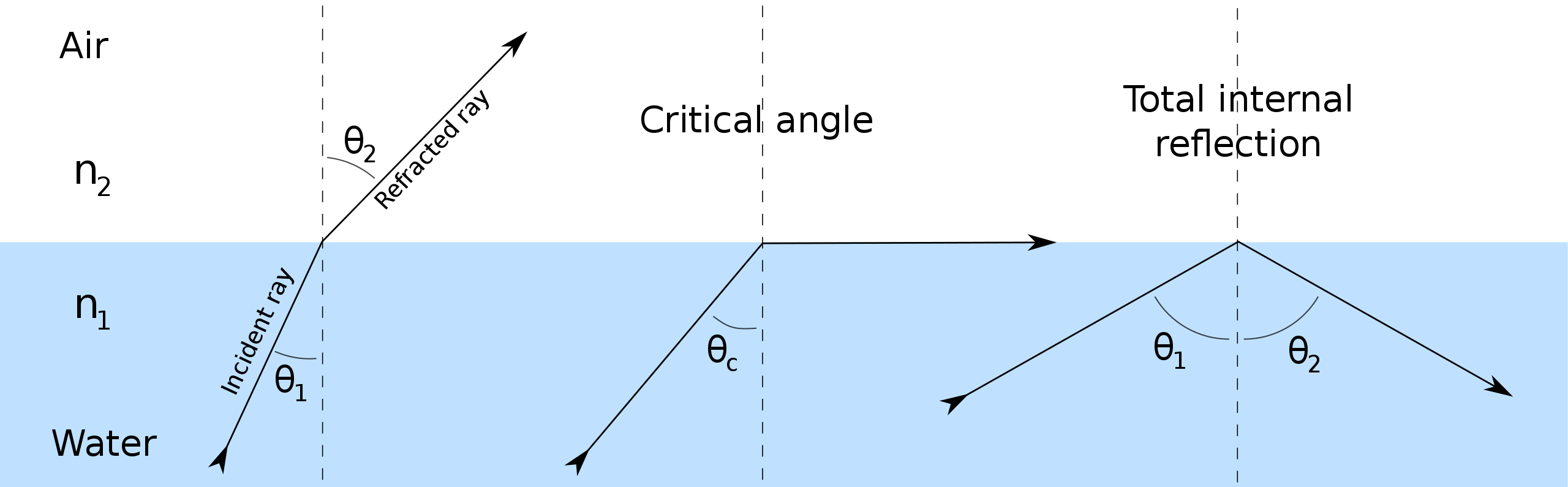
If angle of incidence is smaller than critical angle, most the light passes through.

If the angle of incidence is equal to the critical angle, the light travels across the surface.

If the angle of incidence is greater than the critical angle, the light is reflected back.

Calculating critical angle

Refractive index table

\begin{gather} sin\theta _{C} =\frac{1}{n}\\ n=refractive\ index \notag \end{gather}

Total internal reflection only occurs when the light ray propagates from a optically denser medium to an optically less dense medium.

Diffraction through a single-slit and around objects

Single slit

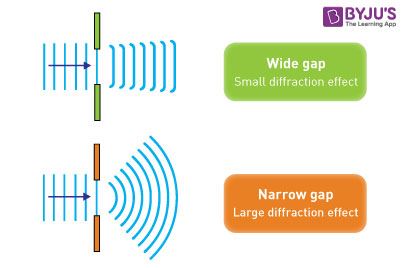
The narrower the gap the larger the diffraction effect

Video demonstration

Diffraction around obstacle

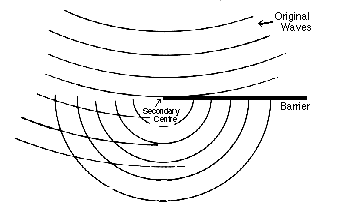
Diffraction is the slight bending of light as it passes around the edge of an object. The amount of bending depends on the relative size of the wavelength of light to the size of the opening. If the opening is much larger than the light's wavelength, the bending will be almost unnoticeable. However, if the two are closer in size or equal, the amount of bending is considerable, and easily seen with the naked eye.

Video demonstration

Interference patterns

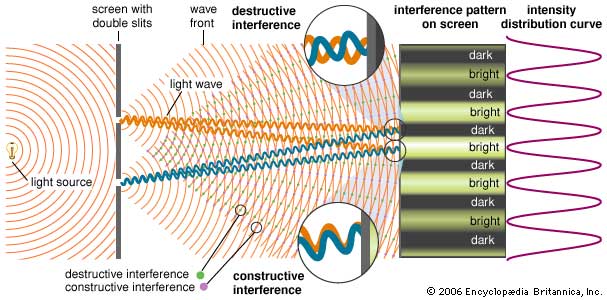
Double-slit interference

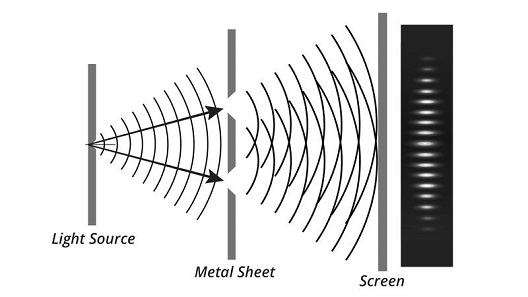Demonstation by Veritasium
Young's experiment

Path difference

Explanation from the Physics classroom

4.5 Standing waves

The nature of standing waves

Standing waves result from the superposition of two opposite waves which are otherwise identical.

Standing waves don't transfer energy.

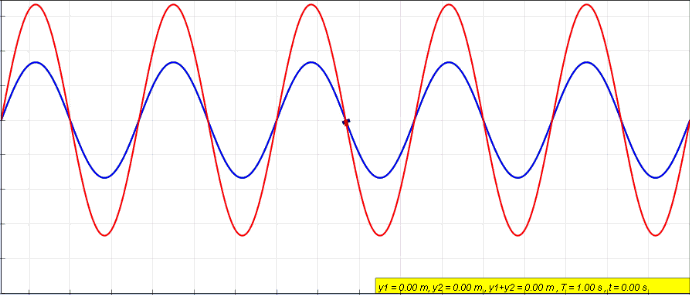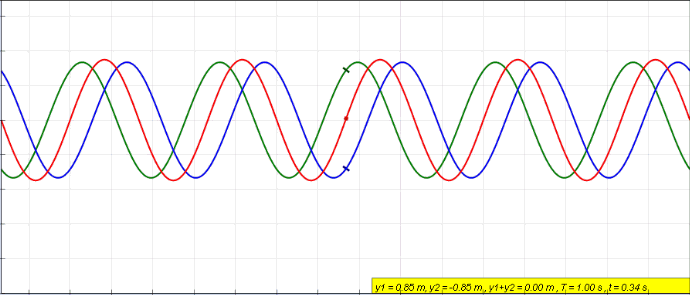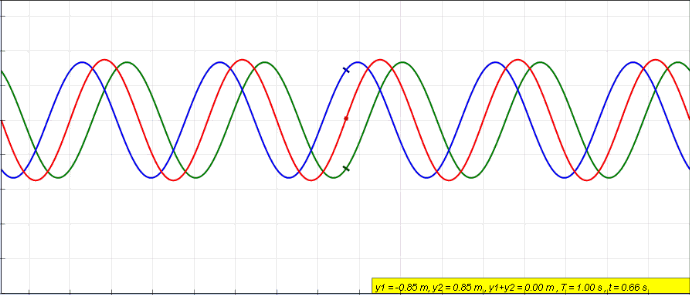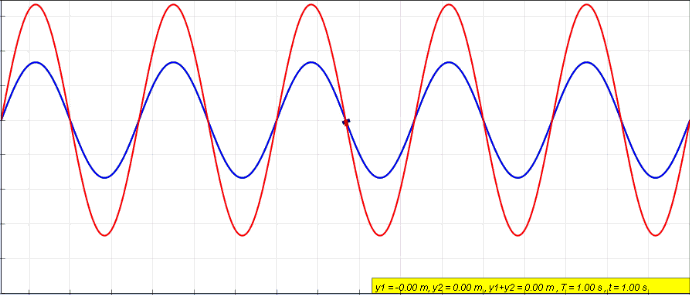
Animation of a standing wave (red) created by the superposition of a left traveling (blue) and right traveling (green) wave

Standing waves demonstration with a slinky

Boundary conditions

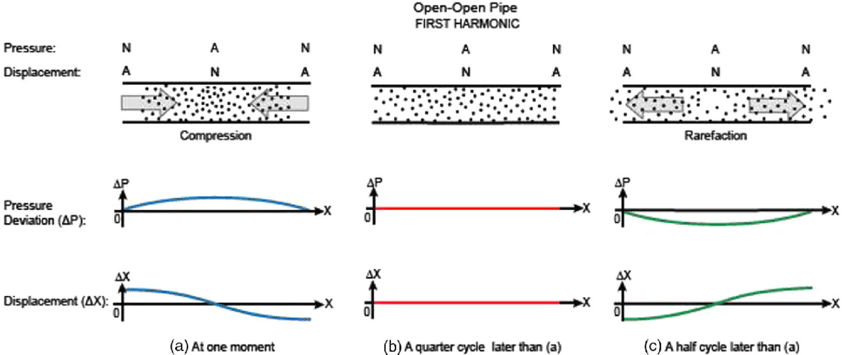
Strings and closed pipes create standing waves in an equivalent way.

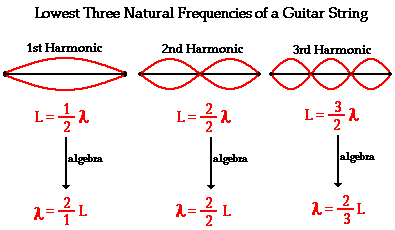
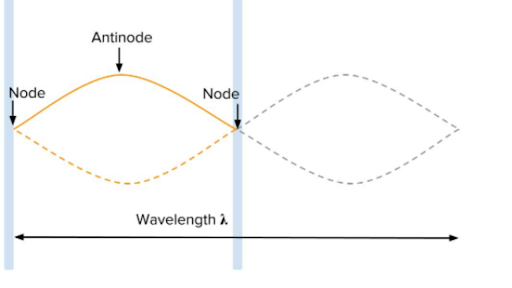
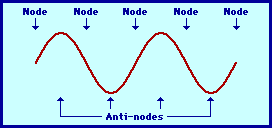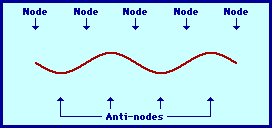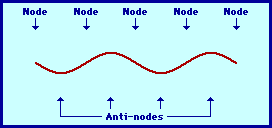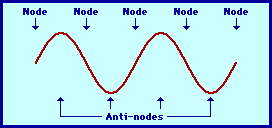
Notes and antinodes

Nodes are fixed positions along a standing wave. Node is the minumum, and antinode is the one with the largest displacement.

The distance between two adjecent nodes is λ/2

Standing waves	Travelling waves
No energy propagated	Energy propagated
Nodes and antinodes	Neither
Amplitude varies along the wave	Amplitude stays constant along the wave
Particles between two adjacent nodes oscillate in phase and particles separated by exactly one node oscillate in antiphase	The phase difference between two particles of a travelling wave can take any value between 0 and 2π